Tính: A = 1 + 7 + 72 + 73 + ... + 72007.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NP
2
20 tháng 9 2023
\(A=7+7+7^2+...+7^{100}\)
\(7A=7^2+7^2+7^3+...+7^{101}\)
\(A=14+7^2+7^{101}\)
VN
Võ Ngọc Phương
VIP
31 tháng 7 2023
\(S=7+7^2+7^3+...7^{20}\)
Ta có: \(7S=7.\left(7+7^2+7^3+...+7^{20}\right)\)
\(7S=7^2+7^3+7^4+...+7^{21}\)
\(7S-S=\left(7^2+7^3+7^4+...+7^{21}\right)-\left(7+7^2+7^3+...+7^{20}\right)\)
\(6S=\left(7^{21}-7\right)\)
\(S=\left(7^{21}-7\right):6\)
Chúc bạn học tốt
PT
1
DD
4
23 tháng 8 2015
A = 1 + 1/110 + 1 + 1/90 + ... + 1 + 1 /2
A = 10 + 1/1.2+ 1 /2.3 + ... + 1/9.10 + 1/10.11
A = 10 + 1/1 - 1/2 + 1 /2 - 1/3 + ... + 1/9 - 1/10 + 1/10 - 1/11
A = 10 + 1/1 - 1/11
A = 10 + 10/11
A = 120/11
HT
23 tháng 8 2015
A = \(\frac{111}{110}+\frac{91}{90}+\frac{73}{72}+...+\frac{13}{12}+\frac{7}{6}+\frac{3}{2}\)
A = \(\left(\frac{1}{2}+1\right)+\left(\frac{1}{6}+1\right)+\left(\frac{1}{12}+1\right)+....+\left(\frac{1}{110}+1\right)\)
A = (1 + 1 + 1 +...+ 1) + \(\left(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+...+\frac{1}{110}\right)\)
A = 10 + \(\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{10.11}\right)\)
A = \(10+\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{10}-\frac{1}{11}\right)\)
A = \(10+\left(1-\frac{1}{11}\right)\)
A = \(10+\frac{10}{11}\)
A = \(\frac{120}{11}\)
28 tháng 12 2022
Ta xét biểu thức \(A_1=7+7^2+7^3\) \(=7\left(1+7+7^2\right)\) \(=57.7⋮57\)
\(A_2=7^4+7^5+7^6\) \(=7^4\left(1+7+7^2\right)\) \(=57.7^4⋮57\)
...
\(A_{40}=7^{118}+7^{119}+7^{120}\) \(=7^{118}\left(1+7+7^2\right)⋮57\)
Vậy \(A=\sum\limits^{40}_{i=1}A_i\) đương nhiên chia hết cho 57 (đpcm)
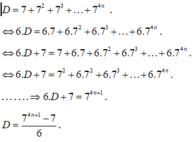
=> 7A=7.(7+72+73+...+72016)
7A=72+73+74+...+72017
=> 7A-A=(72+73+74+...+72017)-(7+72+73+...+72016)
=> 6A=72017-7
=> A=\(\frac{7^{2017}-7}{6}\).
cho mìh hỏi 7^2016 và 7^2017 ở đâu ra vậy bạn