62x-2 ×2 = 72
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PT
1
MT
0
31 tháng 7 2016
sin6(2x)+cos6(2x)=0
<=>(sin22x)3+(cos22s)3=0
<=> (sin22x+cos2x)[(sin42x-2sin22x.cos22x+cos42x)=0
<=>sin42x-2sin22x.cos22x+cos42x=0
đến đây bạn nhóm l;ại và giải
KQ là k có nghiệm
=> PT vô nghiệm
16 tháng 9 2021
b: Ta có: \(6^{2x-1}=216\)
\(\Leftrightarrow2x-1=3\)
hay x=2
c: Ta có: \(x^3=25x\)
\(\Leftrightarrow x\left(x-5\right)\left(x+5\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=5\\x=-5\end{matrix}\right.\)
CM
13 tháng 2 2017
a) 3 x 2 + 8 x + 4 = 0 ;
a = 3; b' = 4; c = 4
Δ ' = ( b ' ) 2 - a c = 4 2 - 3 . 4 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( - 4 + 2 ) / 3 = ( - 2 ) / 3 ; x 2 = ( - 4 - 2 ) / 3 = - 2
b) 7 x 2 - 6 √ 2 x + 2 = 0
a = 7; b' = -3√2; c = 2
Δ ' = ( b ' ) 2 - a c = ( - 3 √ 2 ) 2 - 7 . 2 = 4 ⇒ √ ( Δ ' ) = 2
Phương trình có 2 nghiệm:
x 1 = ( 3 √ 2 + 2 ) / 7 ; x 2 = ( 3 √ 2 - 2 ) / 7
CM
23 tháng 3 2019
a, 5(x – 7) = 0
x – 7 = 0
x = 7
b, 95 – 5(x+2) = 45
5(x+2) = 40
x+2 = 8
x = 6
c, 6 2 x + 2 3 + 40 = 100
6(2x+8) = 60
2x+8 = 10
x = 1
d, 3(3x+9)+6 = 96
3(3x+9) = 90
3x+9 = 30
3x = 27
x = 9
e, 2 6 + 5 + x = 3 4
5+x = 81–64
5+x = 17
x = 12
29 tháng 7 2023
a: \(=\dfrac{6}{3}\cdot x\cdot\dfrac{y^2}{y}=2xy\)
b: \(=\dfrac{62}{2}\cdot\dfrac{x^4}{x^3}\cdot\dfrac{y^3}{y^2}=31xy\)
c: \(=\dfrac{-18}{6}\cdot\dfrac{x^4}{x^2}\cdot\dfrac{y^3}{y}=-3x^2y^2\)
d: \(=\dfrac{27}{9}\cdot\dfrac{x^5}{x^3}\cdot\dfrac{y^6}{y^3}=3x^2y^3\)
e: \(=\dfrac{18}{12}\cdot\dfrac{x^3}{x}\cdot\dfrac{y^4}{y^3}=\dfrac{3}{2}x^2y\)
4 tháng 7 2018
bài làm
62x+3.2x=9.29
62x+6x=261
62+6x=261
68x=261
x=261:68
x=\(\frac{261}{68}\)
5 tháng 3 2020
Ta có : \(6x^4-35x^3+62x^2-35x+6=0\)
=> \(6x^4-3x^3-32x^3+16x^2+46x^2-23x-12x+6=0\)
=> \(3x^3\left(2x-1\right)-16x^2\left(2x-1\right)+23x\left(2x-1\right)-6\left(2x-1\right)=0\)
=> \(\left(3x^3-16x^2+23x-6\right)\left(2x-1\right)=0\)
=> \(\left(3x^3-x^2-15x^2+5x+18x-6\right)\left(2x-1\right)=0\)
=> \(\left(x^2\left(3x-1\right)-5x\left(3x-1\right)+6\left(3x-1\right)\right)\left(2x-1\right)=0\)
=> \(\left(x^2-5x+6\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x^2-2x-3x+6\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x\left(x-2\right)-3\left(x-2\right)\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left(x-3\right)\left(x-2\right)\left(3x-1\right)\left(2x-1\right)=0\)
=> \(\left[{}\begin{matrix}x-3=0\\x-2=0\\3x-1=0\\2x-1=0\end{matrix}\right.\)
=> \(\left[{}\begin{matrix}x=3\\x=2\\x=\frac{1}{3}\\x=\frac{1}{2}\end{matrix}\right.\)
Vậy phương trình có tập nghiệm là \(S=\left\{2,3,\frac{1}{2},\frac{1}{3}\right\}\)
NV
Nguyễn Việt Lâm
Giáo viên
5 tháng 3 2020
Nhận thấy \(x=0\) ko là nghiệm, chia 2 vế của pt cho \(x^2\)
\(6x^2+\frac{6}{x^2}-35x-\frac{35}{x}+62=0\)
\(\Leftrightarrow6\left(x^2+\frac{1}{x^2}\right)-35\left(x+\frac{1}{x}\right)+62=0\)
Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)
\(6\left(t^2-2\right)-35t+62=0\)
\(\Leftrightarrow6t^2-35t+50=0\Rightarrow\left[{}\begin{matrix}t=\frac{5}{2}\\t=\frac{10}{3}\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=\frac{5}{2}\\x+\frac{1}{x}=\frac{10}{3}\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}2x^2-5x+2=0\\3x^2-10x+3=0\end{matrix}\right.\)
CM
6 tháng 1 2019
Ta có: x 2 - 6 2 x + 18 = x - 3 2 2 ≥ 0 ∀ x
Tập nghiệm của bất phương trình x 2 - 6 2 x + 18 ≥ 0 là S= R.
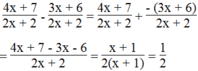
6^2x-2 x 2 =72
6^2x-2 = 36
6^2x-2 =6^2
2x-2=2
2x=4
x=2
\(6^{2x-2}.2=72\)
\(6^{2x-2}=72:2\)
\(6^{2x-2}=36\)
\(6^{2x-2}=6^2\)
\(\Leftrightarrow2x-2=2\)
\(\Leftrightarrow2x=2+2\)
\(\Leftrightarrow2x=4\)
\(\Leftrightarrow x=4:2\)
\(\Leftrightarrow x=2\)
Vậy \(x=2\)