Làm phép chia
1 . (3x3-8x2+3x+2) : (3x+1)
2. (2x4+3x3_16x2+6x+45) : ( 2x+3)
help me <3
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
Ta có:
$2x^4-3x^3-3x-2=2x^2(x^2-1)-3x(x^2-1)+2x^2-6x-2$
$=(2x^2-3x)(x^2-1)+2(x^2-1)-6x$
$=(2x^2-3x+2)(x^2-1)-6x$
Vậy $2x^4-3x^3-3x-2$ chia $x^2-1$ dư $-6x$
Không có đáp án nào đúng

Ta có: \(\dfrac{4x^4+3x^3}{-x^3}+\dfrac{15x^2+6x}{3x}=0\)
\(\Leftrightarrow-4x-3+5x+2=0\)
\(\Leftrightarrow x-1=0\)
hay x=1

1: Sửa đề: 3x-5
\(=\dfrac{-x^2\left(3x-5\right)-3\left(3x-5\right)}{3x-5}=-x^2-3\)
2: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
=5x^2+14x^2+12x+8
3: \(=\dfrac{5x^3+10x^2+4x^2+8x+4x+8}{x+2}=5x^2+4x+4\)
4: \(=\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}=x^2+1-2x\)
5: \(=\dfrac{x^2\left(5-3x\right)+3\left(5-3x\right)}{5-3x}=x^2+3\)

Thực hiện phép chia \(a\left(x\right)=x^3+2x^2+3x-1\) cho \(b\left(x\right)=x-2\), ta được:
\(a\left(x\right)=\left(x-2\right)\cdot Q\left(x\right)+r\)
\(\Rightarrow a\left(2\right)=\left(2-2\right)\cdot Q\left(2\right)+r=r\)
\(\Rightarrow r=2^3+2\cdot2^2+3\cdot2-1=21\)
Vậy số dư phép chia \(a\left(x\right)\) cho \(b\left(x\right)\) là \(21\).

2x4 – 3x3 – 3x2 – 2 + 6x = 2x4 – 3x3 – 3x2 + 6x – 2
Thực hiện phép chia:
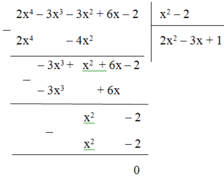
Vậy (2x4 – 3x3 – 3x2 + 6x – 2) : (x2 – 2) = 2x2 – 3x + 1.

\(\frac{x^4+x^3+6x^2+5x+5}{x^2+x+1}=\frac{x^4+x^3+x^2+5x^2+5x+5}{x^2+x+1}=\frac{x^2\left(x^2+x+1\right)+5\left(x^2+x+1\right)}{\left(x^2+x+1\right)}=\frac{\left(x^2+x+1\right)\left(x^2+5\right)}{x^2+x+1}=x^2+5\)
\(\frac{x^4+x^3+2x^2+x+1}{x^2+x+1}=\frac{x^4+x^3+x^2+x^2+x+1}{x^2+x+1}=\frac{x^2\left(x^2+x+1\right)+\left(x^2+x+1\right)}{x^2+x+1}=\frac{\left(x^2+x+1\right)\left(x^2+1\right)}{x^2+x+1}=x^2+1\)
3x^3-8x^2+3x+2 3x+1 x^2-3x+2 3x^3+x^2 - -9x^2+3x+2 -9x^2-3x - 6x+2 6x+2 - 0
Vậy (3x3-8x2+3x+2) : (3x+1) \(=x^2-3x+2\)