Gọi x là nghiệm dương nhỏ nhất của phương trình 2cos2x/1-sin2x=0.mệnh đề nào sau đây đúng
A,x€{0;π/4}
B,x€[π\4;π\2]
C,x€{π\2;3π\4}
D,x€[3π\4;π]
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án C

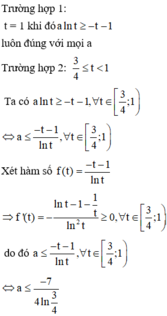
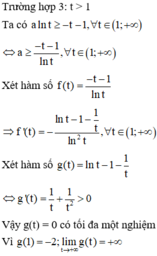
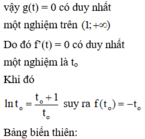

Vậy số thực a thỏa mãn yêu cầu bài toán là: a ∈ ( 6 ; 7 ]

Đáp án A.
Đặt t = x 2 − x + 1 = x − 1 2 2 + 3 4 ≥ 3 4
Khi đó BPT trở thành
f t = t + 1 + a ln t ≥ 0
Ta có: f ' t = + ∞ ; f 3 4 = 3 4 + a ln 3 4
Với a > 0 ⇒ f t đồng biến trên
3 4 ; + ∞ ⇒ f t ≥ 0 ∀ t ∈ 3 4 ; + ∞ ⇔ M i n 3 4 ; + ∞ f t = 7 4 + a
⇔ a ln 3 4 ≥ − 7 4 ⇔ a ≤ − 7 4 ln 3 4 ≈ 6 , 08.
Vì đề bài yêu cầu tìm số thực lớn nhất
nên suy ra a ∈ 6 ; 7 .

Đáp án B
Đặt 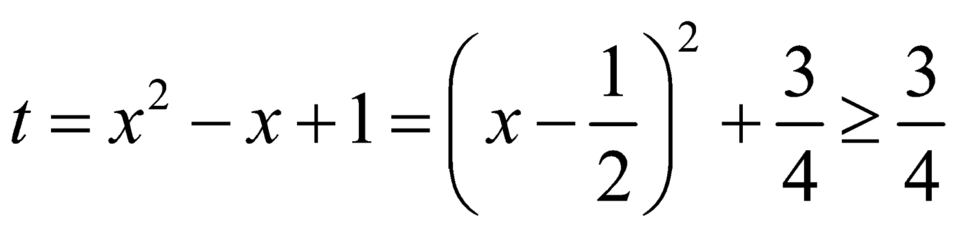
Ta có:
![]()
![]()
Đặt ![]() .
.
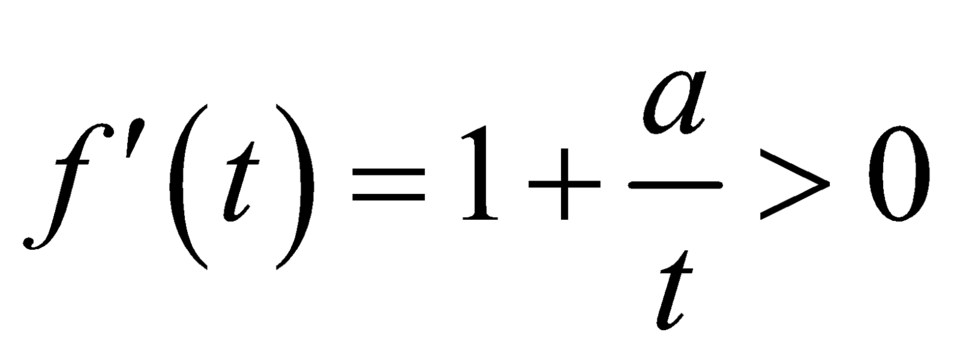
![]() là hàm số đồng biến trên
là hàm số đồng biến trên 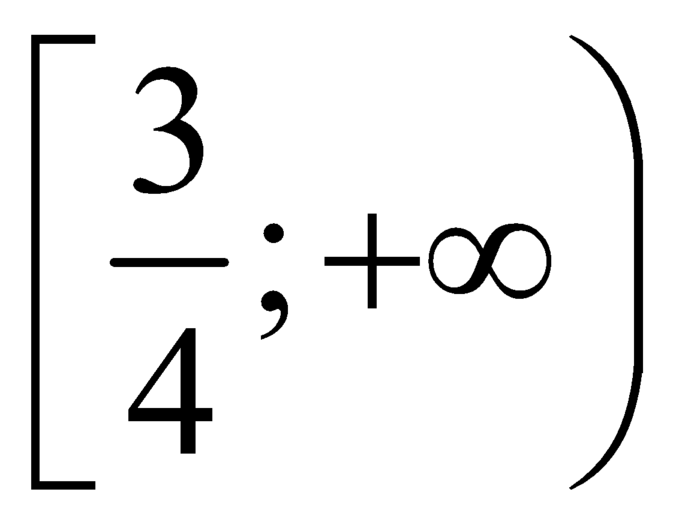 .
.
Khi đó 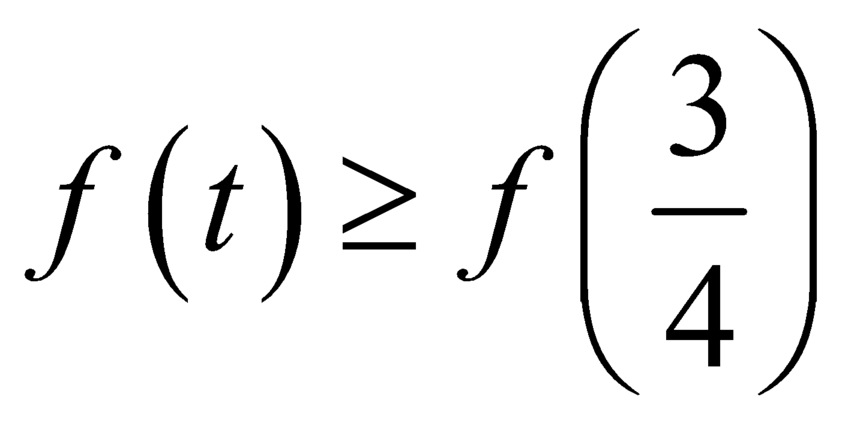
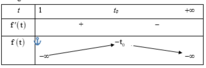
![]()
![]()
![]()

Phương trình:
3 sin 2 x + 2 sin x cos x - cos 2 x = 0 (*).
cos x = 0 ⇒ sin 2 x = 1 không phải là nghiệm của phương trình (*).
cos x ≠ 0 . Ta có:
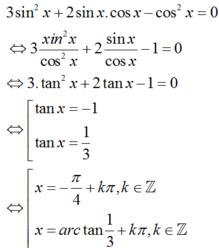
Nghiệm nguyên dương nhỏ nhất của phương trình là x 0 ∈ 0 ; π 2
Chọn C.
ĐKXĐ: \(x\ne\frac{\pi}{4}+k\pi\)
\(cos2x=0\Rightarrow2x=\frac{k\pi}{2}\Rightarrow x=\frac{k\pi}{4}\)
Kết hợp ĐKXĐ \(\Rightarrow x=-\frac{\pi}{4}+k\pi\)
\(\Rightarrow\) Nghiệm dương nhỏ nhất là \(x=\frac{3\pi}{4}\)
Đáp án D đúng
Cos và sin không có đk mà