\((m-1)x^2-2(m-4)x+m-5=0\)
tìm hệ thức liên hệ giữa \(x \)1, \(x \)2 k phụ thuộc vào m
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 7 2017
a, Để phương trình có 2 nghiệm \(x_1,x_2\)thì \(\Delta=\left(m-1\right)^2-\left(2m-4\right)=m^2-4m+5>0\)
Dễ thấy \(\Delta\ge1\forall m\)nên phương trình luôn có 2 nghiệm phân biệt
Theo hệ thức Viet ta có \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1.x_2=2m-4\end{cases}}\)
\(\left|x_1-x_2\right|=4\Rightarrow\left(x_1-x_2\right)^2=16\Rightarrow\left(x_1+x_2\right)^2-4x_1x_2=16\)
\(\Rightarrow4\left(m^2-2m+1\right)-4\left(2m-4\right)=16\)\(\Rightarrow m^2+2m-1=0\Rightarrow\orbr{\begin{cases}m=-1+\sqrt{2}\\m=-1-\sqrt{2}\end{cases}}\)
b. Ta có \(\hept{\begin{cases}x_1+x_2=2m-2\\x_1.x_2=2m-4\end{cases}\Rightarrow x_1+x_2-x_1.x_2}=2\)
VH
2
HP
30 tháng 8 2021
Theo định lí Vi-ét:
\(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=-m\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1+x_2=2m+2\\2x_1x_2=-2m\end{matrix}\right.\)
\(\Rightarrow x_1+x_2+2x_1x_2=2\)
NV
Nguyễn Việt Lâm
Giáo viên
30 tháng 8 2021
Học sinh đã có 5 điểm, chỉ xét 25 câu còn lại thì học sinh cần có số điểm từ 1 đến 3, gọi x là số câu đúng với \(0\le x\le25\)
Với mỗi câu đúng có 0,2 điểm nên ta có:
\(1< 0,2x\le3\Rightarrow5< x\le15\)
\(\Rightarrow x=\left\{6;7;...;15\right\}\)
Do đó xác suất sẽ là: \(\sum\limits^{15}_{k=6}\left(\dfrac{1}{4}\right)^k\left(\dfrac{3}{4}\right)^{25-k}.C_{25}^k\approx0,622\) (bấm tổng trong casio nó tính 3s xong)
NV
Nguyễn Việt Lâm
Giáo viên
31 tháng 1 2021
Coi như pt đã cho có 2 nghiệm, khi đó: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{-2m^2+2}{m^2+1}=-2+\dfrac{4}{m^2+1}\\x_1x_2=\dfrac{m}{m^2+1}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}x_1+x_2+2=\dfrac{4}{m^2+1}\\x_1x_2=\dfrac{m}{m^2+1}\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m^2+1=\dfrac{4}{x_1+x_2+2}\\x_1x_2=\dfrac{m}{m^2+1}=\dfrac{m}{4}\left(x_1+x_2+2\right)\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}m^2=\dfrac{2-x_1-x_2}{x_1+x_2+2}\\x_1x_2=\dfrac{m}{4}\left(x_1+x_2+2\right)\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\pm\dfrac{1}{4}\left(x_1+x_2+2\right)\sqrt{\dfrac{2-x_1-x_2}{x_1+x_2+2}}\)
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 5 2021
Phương trình có 2 nghiệm pb khi:
\(\Delta'=\left(m+1\right)^2-m^2>0\Leftrightarrow2m+1>0\)
\(\Rightarrow m>-\dfrac{1}{2}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=m^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\dfrac{x_1+x_2-2}{2}=m\\x_1x_2=m^2\end{matrix}\right.\)
\(\Rightarrow x_1x_2=\left(\dfrac{x_1+x_2-2}{2}\right)^2\)
Đây là hệ thức liên hệ 2 nghiệm ko phụ thuộc m
9 tháng 5 2021
a,Phương trình có 2 nghiệm pb khi: \(\Delta'>0\Rightarrow\left(m+1\right)^2-m^2>0\Leftrightarrow2m+1>0\Leftrightarrow m>\dfrac{-1}{2}\)
26 tháng 2 2022
\(x^2+2x-1-m^2=0\Leftrightarrow\left(x-1\right)^2=m^2\)
\(\Leftrightarrow x-1=\sqrt{m^2}=\left|m\right|\)
\(\Leftrightarrow\left[{}\begin{matrix}x-1=m\\x-1=-m\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=1+m\\x=1-m\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x_1=1+m\\x_2=1-m\end{matrix}\right.\)
CM
21 tháng 8 2019
b) Theo định lí Vi-et ta có:
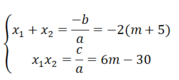
⇒ 3( x 1 + 2 ) + x 1 x 2 = -6(m + 5) + 6m - 30
= -6m - 30 + 6m - 30 = -60
Vậy hệ thức liên hệ giữa 2 nghiệm không phụ thuộc vào giá trị của m là
3( x 1 + x 2 ) + x 1 x 2
13 tháng 3 2023
a: Thay x=5 vào pt, ta được:
5^2-2(m-1)*5+m^2-4m+3=0
=>m^2-4m+3+25-10m+10=0
=>m^2-14m+38=0
=>(m-7)^2=11
=>\(m=\pm\sqrt{11}+7\)
b: x1+x2=2m-2
x1*x2=m^2-4m+3
(x1+x2)^2-4x1x2
=4m^2-8m+4-4m^2+4m-6
=-4m-2
(x1+x2)^2-4x1x2+2(x1+x2)
=-4m-2+4m-4=-6
AH
Akai Haruma
Giáo viên
12 tháng 2 2023
Lời giải:
a. Áp dụng định lý Viet, với $x_1,x_2$ là nghiệm của pt thì:
$x_1+x_2=m+2$
$x_1x_2=m-1$
$\Rightarrow x_1+x_2-x_1x_2=(m+2)-(m-1)=3$
$\Leftrightarrow x_1+x_2-x_1x_2-3=0$ (đây chính là biểu thức liên hệ giữa $x_1,x_2$ mà không phụ thuộc vào $m$)
b.
$x_1+x_2=-(4m+1)$
$x_1x_2=2(m-4)$
$\Rightarrow x_1+x_2+2x_1x_2=-(4m+1)+4(m-4)=-17$
$\Rightarrow x_1+x_2+2x_1x_2+17=0$
15 tháng 5 2020
a) PT có 2 nghiệm dương
\(\Leftrightarrow\hept{\begin{cases}\Delta'>0\\P>0\\S>0\end{cases}\Leftrightarrow\hept{\begin{cases}\left(m+3\right)^2-\left(4m-1\right)\ge0\\4m-1>0\\2\left(m+3\right)>0\end{cases}}\Leftrightarrow\hept{\begin{cases}m^2+2m+10\ge0\\m>\frac{1}{4}\\m>-3\end{cases}}}\)
\(\Leftrightarrow m>\frac{1}{4}\)
b) vì \(\Delta'>0\)nên PT đã cho luôn có hai nghiệm x1,x2 với mọi m.
Áp dụng hệ thức Vi-et,ta có :
\(\hept{\begin{cases}S=2\left(m+3\right)\\P=4m-1\end{cases}}\Leftrightarrow\hept{\begin{cases}2S=4m+12\\P=4m-1\end{cases}}\)
\(\Leftrightarrow2S-P=13\Leftrightarrow2\left(x_1+x_2\right)-x_1x_2=13\)
Với \(m\ne1\), giả sử pt đã cho có 2 nghiệm, theo Viet ta có:
\(\left\{{}\begin{matrix}x_1+x_2=\frac{2\left(m-4\right)}{m-1}\\x_1x_2=\frac{m-5}{m-1}\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2\left(x_1+x_2\right)=\frac{4m-16}{m-1}\\-3x_1x_2=\frac{-3m+15}{m-1}\end{matrix}\right.\)
Cộng vế với vế:
\(2\left(x_1+x_2\right)-3x_1x_2=\frac{m-1}{m-1}=1\)
\(\Rightarrow2\left(x_1+x_2\right)-3x_1x_2-1=0\)
Đây là biểu thức liên hệ 2 nghiệm ko phụ thuộc m