cho tam giác ABC trực tâm H, các đường thẳng vuông góc với AB tại B, vuông góc với AC tại C và chúng cắt nhau tại D.tứ giác BDCH là hình bình hành,Chứng minh rằng
a/ tính góc bcd biết góc bac = 60 độ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

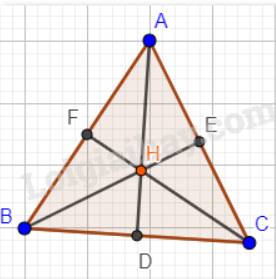
Giả sử tam giác ABC có H vừa là trực tâm, vừa là trọng tâm tam giác ABC. Ta phải chứng minh tam giác ABC đều.
Vì H là trọng tâm tam giác ABC nên AD, BE, CF vừa là các đường cao, vừa là các đường trung tuyến trong tam giác.
Suy ra: AF = BF = AE = CE = BD = CD;
\(AD \bot BC; BE \bot AC; CF \bot AB\)
Xét tam giác ADB và tam giác ADC có:
AD chung
\(\widehat{ADB}=\widehat{ADC} (=90^0)\)
BD = CD (D là trung điểm của đoạn thẳng BC).
Vậy \(\Delta ADB = \Delta ADC\)(c.g.c) nên AB = AC ( 2 cạnh tương ứng).
Tương tự, ta cũng được, AC = BC
Xét tam giác ABC có AB = AC = BC nên là tam giác đều.
Vậy tam giác ABC có trực tâm H cũng là trọng tâm của tam giác thì tam giác ABC đều.

Trong ΔABC ta có H là trực tâm nên:
AH ⊥ BC, BH ⊥ AC, CH ⊥ AB
Trong ΔAHB, ta có:
AC ⊥ BH
BC ⊥ AH
Vì hai đường cao kẻ từ A và B cắt nhau tại C nên C là trực tâm của tam giác AHB.
Trong ΔHAC, ta có:
AB ⊥ CH
CB ⊥ AH
Vì hai đường cao kẻ từ A và C cắt nhau tại B nên B là trực tâm của ΔHAC.
Trong ΔHBC, ta có:
BA ⊥ HC
CA ⊥ BH
Vì hai đường cao kẻ từ B và C cắt nhau tại A nên A là trực tâm của tam giác HBC.

Giải
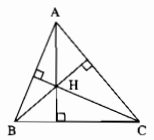
Trong ∆ABC ta có H là trực tâm nên
\(\text{ AH⊥BC,BH⊥AC,CH⊥AB}\)
Trong ∆AHB ta có:
\(\text{AC⊥BH }\)
\(\text{BC⊥AH}\)
Hai đường cao kẻ từ A và B cắt nhau tại C.
Vậy C là trực tâm của ∆AHB.
Trong ∆HAC ta có:
\(\text{BA⊥CH}\)
\(\text{CB⊥BH}\)
Hai đường cao kẻ từ A và C cắt nhau tại B, Vậy B là trực tâm của ∆HAC.
Trong ∆HBC ta có:
\(\text{BA⊥HC}\)
\(\text{CA⊥BH}\)
Hai đường cao kẻ từ B và C cắt nhau tại A. Vậy A là trực tâm của ∆HBC.

Tham khảo:
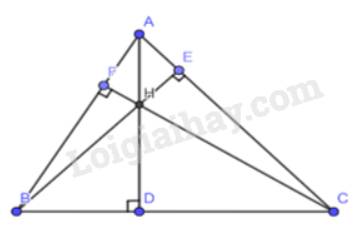
+) Xét tam giác HBC ta có :
HD vuông góc với BC \( \Rightarrow \) HD là đường cao tam giác HBC
BF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)BF là đường cao của tam giác HBC
CE vuông góc với HB tại E ( kéo dài HB ) \( \Rightarrow \)CE là đường cao của tam giác HBC
Ta kéo dài HD, BF, CE sẽ cắt nhau tại A
\( \Rightarrow \) A là trực tâm tam giác HBC
+) Xét tam giác HAB ta có :
HF vuông góc với AB \( \Rightarrow \) HF là đường cao tam giác HAB
BH vuông góc với AE tại E ( kéo dài HB ) \( \Rightarrow \)AE là đường cao của tam giác HAB
BD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)BD là đường cao của tam giác HAB
Ta kéo dài HF, BD, AE sẽ cắt nhau tại C
\( \Rightarrow \) C là trực tâm tam giác HAB
+) Xét tam giác HAC ta có :
HE vuông góc với AC \( \Rightarrow \) HE là đường cao tam giác HAC
AF vuông góc với HC tại F ( kéo dài HC ) \( \Rightarrow \)AF là đường cao của tam giác HAC
CD vuông góc với AH tại D ( kéo dài AH ) \( \Rightarrow \)CD là đường cao của tam giác HAC
Ta kéo dài CD, HE, AF sẽ cắt nhau tại B
\( \Rightarrow \) B là trực tâm tam giác HAC.

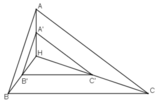
+ ΔABC nhọn ⇒ trực tâm H nằm trong ΔABC.
+ Gọi A’ = V(H; ½) (A)
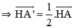
⇒ A’ là trung điểm AH.
+ Tương tự :
B’ = V(H; ½) (B) là trung điểm BH.
C’ = V(H; ½) (C) là trung điểm CH.
⇒ V(H; ½)(ΔABC) = ΔA’B’C’ với A’; B’; C’ là trung điểm AH; BH; CH.

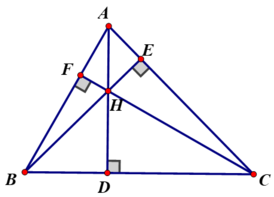
Gọi D, E, F là chân các đường vuông góc kẻ từ A, B, C của ΔABC.
⇒ AD ⟘ BC, BE ⟘ AC, CF ⟘ AB.
ΔHBC có :
AD ⊥ BC nên AD là đường cao từ H đến BC.
BA ⊥ HC tại F nên BA là đường cao từ B đến HC
CA ⊥ BH tại E nên CA là đường cao từ C đến HB.
AD, BA, CA cắt nhau tại A nên A là trực tâm của ΔHCB.