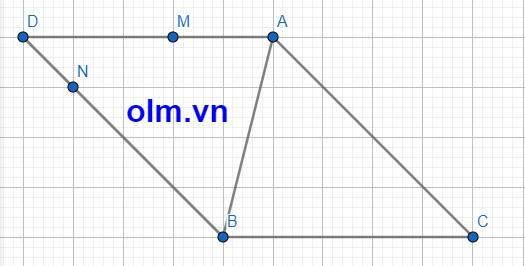
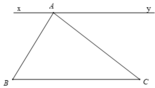
cho tam giác ABC và d đi qua A, song song với BC. gọi B' là điểm đối xứng với B qua d. cmr AB+AC\(\ge\sqrt{a^2+4h^2}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
20 tháng 12 2021
a: Xét tứ giác ABCD có
AD//BC
AB//CD
Do đó: ABCD là hình bình hành
Suy ra: AB=CD
CM
7 tháng 12 2018
a) Có xy // BC (có hai góc so le trong bằng nhau), mà d // BC nên theo tiên đề Ơ-clit suy ra xy trùng với BC.
b) xy có thể trùng với d hoặc không ( xy trùng với d khi Δ A B C có A B C ^ = A C B ^ )
10 tháng 1 2023
a: Xét ΔABD và ΔEDB có
góc ABD=góc EDB
DB chung
góc ADB=góc EBD
Do đó: ΔABD=ΔEDB
b: Xét tứ giác ABED có
AB//ED
AD//BE
Do đó: ABED là hình bình hành
=>AE cắt BD tại trung điểm của mỗi đường
=>IA=IE