phần b giúp ik b
b
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a)
\(\left\{{}\begin{matrix}3x+y=7\left(1\right)\\x-2y=5\left(2\right)\end{matrix}\right.\)
lấy (1) . 2 + (2)
<=> 7x = 19 => x = \(\dfrac{19}{7}\)
thay x = \(\dfrac{19}{7}\) vào phương trình (2) ta có
\(\dfrac{19}{7}\) - 2y = 5
<=> 2y = \(\dfrac{-16}{7}\) => y = \(\dfrac{-8}{7}\)
vậy (x;y) = { ( \(\dfrac{19}{7}\);\(\dfrac{-8}{7}\) ) }
b)
\(\left\{{}\begin{matrix}3x+2y=7\left(1\right)\\2x-y=3\left(2\right)\end{matrix}\right.\)
lấy (2).2 + (1)
=> 7x = 13 => x = \(\dfrac{13}{7}\)
thay x = \(\dfrac{13}{7}\) vào phương trình 2 ta có
\(\dfrac{13}{7}\) - 2y = 5
<=> 2y = \(\dfrac{-22}{7}\) => y = \(\dfrac{-11}{7}\)
vậy (x;y) = {(\(\dfrac{13}{7}\);\(\dfrac{-11}{7}\))}

Xét ΔKIH có MD//IH
nên IM/IK=HD/HK
Xét ΔHKI có DN//KI
nên IN/IH=KD/KH
IM/IK+IN/ID
=HD/HK+DK/KH
=HK/HK=1


\(B=\left[\left(4x^2+4xy+y^2\right)+2\left(2x+y\right)+1\right]+\left(x^2+2x+1\right)+5\\ B=\left(2x+y+1\right)^2+\left(x+1\right)^2+5\ge5\\ B_{min}=5\Leftrightarrow\left\{{}\begin{matrix}2x+y+1=0\\x+1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=1\end{matrix}\right.\)


Bài 4 :

a) Xét \(\Delta AMB\) và \(\Delta AMC\) có :
AB = AC (gt)
\(AM:chung\)
\(BM=MC\left(gt\right)\)
=> \(\Delta AMB\) = \(\Delta AMC\) (c.c.c)
Xét \(\Delta ABC\) có :
AB = AC (gt)
=> \(\Delta ABC\) cân tại A
Mà có : M là trung điểm của BC
Thì : AM là đường trung tuyến trong tam giác cân
=> AM đồng thời là đường trung trực trong tam giác (tính chất tam giác cân)
\(\Rightarrow AM\perp BC\) (đpcm)
b) Xét \(\Delta ADF\) và \(\Delta CDE\) có :
\(AD=DC\left(gt\right)\)
\(\widehat{ADF}=\widehat{CDE}\) (đối đỉnh)
\(FD=DE\left(gt\right)\)
=> \(\Delta ADF\) = \(\Delta CDE\) (c.g.c)
=> \(\widehat{FAD}=\widehat{ECD}\) (2 góc tương ứng)
Mà 2 góc này ở vị trí so le trong
=> \(\text{AF // EC}\) (đpcm)

a: BC=căn 5^2+12^2=13(cm)
Vì AB<AC
nên góc C<góc B
b: Xét ΔBAD có
BH vừa là đường cao, vừa là trung tuyến
nên ΔBAD cân tại B
=>BC là phân giác của góc ABD
Xét ΔBAC và ΔBDC có
BA=BD
góc ABC=góc DBC
BC chung
=>ΔBAC=ΔBDC
=>góc BDC=90 độ và góc BCA=góc BCD
=>CB là phân giác của góc ACD
c: Xét ΔHDM vuông tại H và ΔHAC vuông tại H có
HD=HA
góc HDM=góc HAC
=>ΔHDM=ΔHAC
=>HM=HC
=>H là trung điểm của MC
=>AD là trung trực của MC
d: Xét tứ giác AMDC có
AM//DC
AM=DC
=>AMDC là hình bình hành
=>CD//AM
=>BN vuông góc DC
mà BD vuông góc DC
nên B,N,D thẳng hàng

ý bạn bảo (x-2 và 1 phần 2) là hợp số hả :
ta có (x-2 và 1 phần 2) nhân (2x+3 và 1 phần 5) =0
\(\Leftrightarrow\) [2.(x-2) +1]. [5.(2x+3)+1]=0
\(\Leftrightarrow\)(2x-3)(10x+16)=0
\(\Leftrightarrow\)\(\orbr{\begin{cases}2x=3\\10x=-16\end{cases}}\)\(\Leftrightarrow\)\(\orbr{\begin{cases}x=\frac{3}{2}\\x=\frac{-8}{5}\end{cases}}\)
vậy
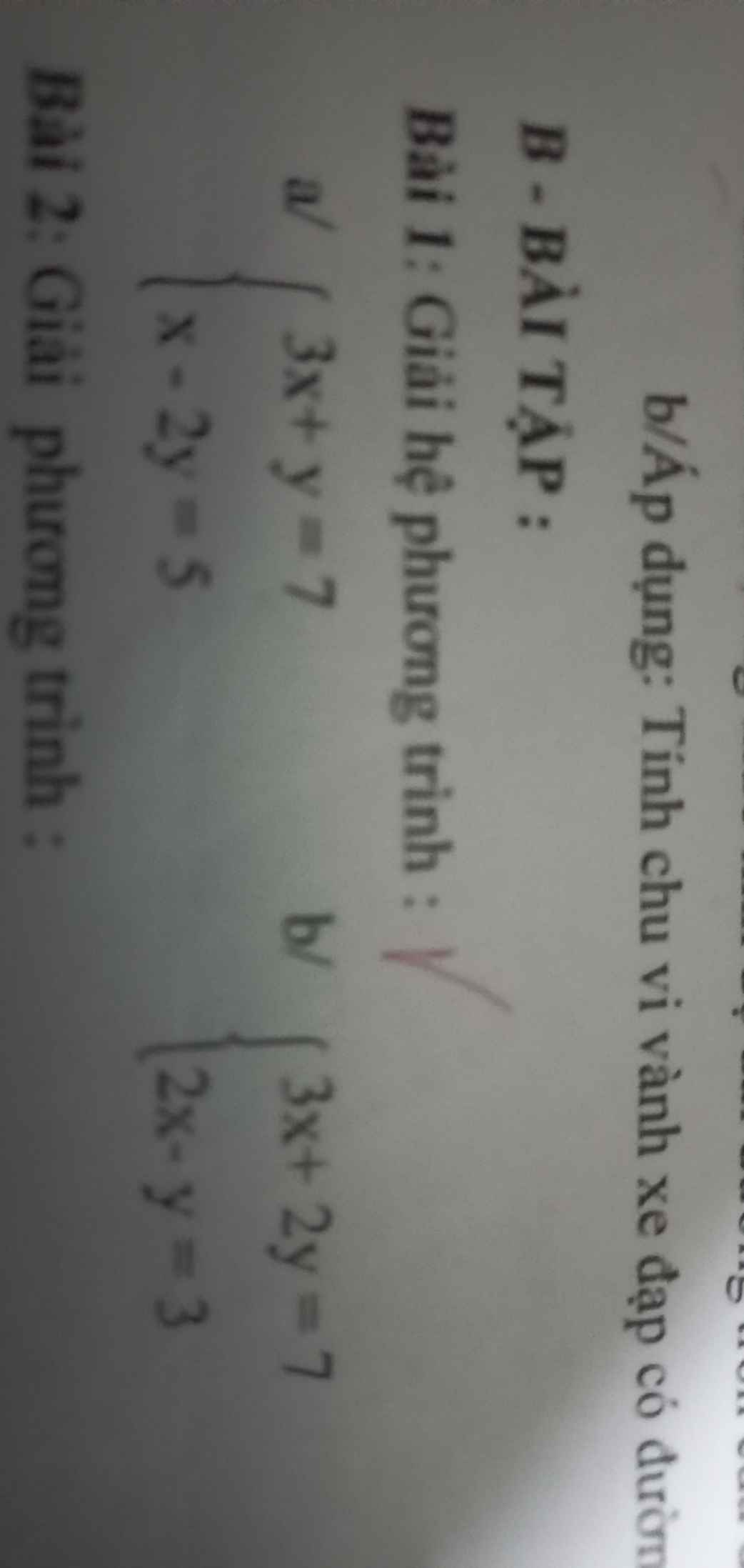





tienganh123 hehehehe
ai lm hộ mk đi