Tìm giá trị lớn nhất và giá trị nhỏ nhất của hàm số:
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Sử dụng công thức lượng giác để biến đổi hàm số về dạng: f t = 2 - 3 4 t 1 - 1 2 t
Đặt t = sin 2 2 x ; 0 ≤ t ≤ 1
Xét hàm số f t = 2 - 3 4 t 1 - 1 2 t = 3 t - 8 2 t - 8 ; t ∈ [0;1].
Ta có f ' t = - 8 2 t - 8 2 < 0 , ∀ t ∈ 0 ; 1 nên f(t) đồng biến trên [ 0;1 ].
Do đó M = f(0) = 1; m = f(1) = 5 6
Vậy 5 M - 6 m - 1 2017 = 5 - 5 - 1 2017 = -1
Đáp án D

bạn nên đưa hàm số về dạng y=|sin8x| +3 rồi mới đánh giá
ta bắt đầu từ 0≤|sin8x|≤10≤|sin8x|≤1
⇔0+3≤y=|sin8x|+3≤1+3⇔0+3≤y=|sin8x|+3≤1+3
3≤y≤43≤y≤4
vậy GTLN =4 đạt được khi sin8x =1
GTNN=3 đạt được khi sin8x =0

Đáp án là D.
Ta có:
y = sin 4 x + cos 2 x + 2 y = sin 4 x − sin 2 x + 3
Đăt t = sin 2 x , t ∈ 0 ; 1
f ( t ) = t 4 − t 2 + 3 ⇒ f ' ( t ) = 4 t 3 − 2 t ⇒ f ' ( t ) = 0 ⇔ t = 0 ∈ [ 0 ; 1 ] t = 2 2 ∈ [ 0 ; 1 ] t = − 2 2 ∉ [ 0 ; 1 ] ⇒ f ( 0 ) = 3 ; f ( 1 ) = 3 ; f 2 2 = 11 4
Vậy giá trị nhỏ nhất của hàm số đã cho là: 11 4
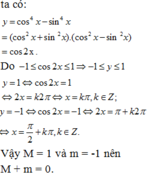
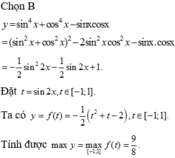
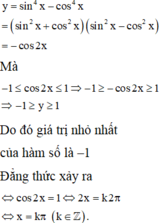
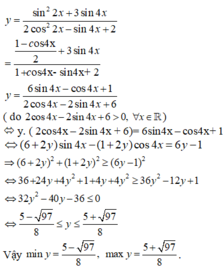

\(f\left(x\right)=sin^4x+cos^4x=sin^4x+2sin^2xcos^2x+cos^4x-2sin^2xcos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-\frac{1}{2}sin^22x=1-\frac{1}{2}sin^22x\)
Ta có: \(0\le sin^22x\le1\)
suy ra \(\frac{1}{2}\le f\left(x\right)\le1\).