Question

[Trần Thị Hằng]

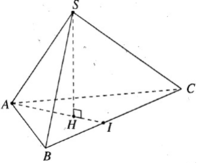
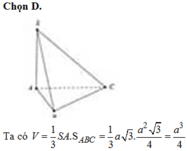
Bài 1:Cho khối chóp tam giác đều S.ABC có các cạnh bên bằng a; và góc giữa cạnh bên và cạnh đáy\(60^o\). Tính thể tích khối chóp S.ABC

Bài 2: Cho hình chóp tứ giác đều S.ABCD có đường cao bằng a và các mặt bên là các tam giác cân có góc ở đỉnh bằng \(60^o\). Tính thể tích khối chóp S.ABCD

Bài 3: Cho hình chóp S.ABCD có đáy ABCD là hình thang vuông tại A,hai đáy là AD=2a, BC=a. Biết AB=a, SA=a và \(SA\perp\left(ABCD\right)\)

1. Tính thể tích của khối chóp S.ACD

2. Tính thể tích của khối chóp S>BCD và khoảng cách s(B;(SCD))

Answer 1

[Nguyễn Việt Lâm]

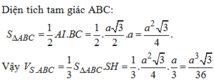
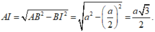
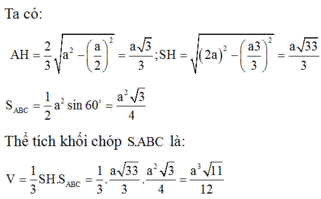
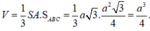
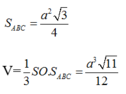
Người đọc tự vẽ hình :D
Câu 1: Đề là góc giữa cạnh bên và cạnh đáy chứ ko phải mặt đáy đúng ko?

Do góc giữa cạnh bên và cạnh đáy bằng \(60^0\) nên các mặt bên là các tam giác đều

\(\Rightarrow SA=SB=SC=AB=a\)

Gọi H là hình chiếu vuông góc của S lên đáy \(\Rightarrow AH=\frac{2}{3}.\frac{a\sqrt{3}}{2}=\frac{a\sqrt{3}}{3}\)

\(\Rightarrow SH=\sqrt{SA^2-AH^2}=\frac{a\sqrt{6}}{3}\)

\(\Rightarrow V=\frac{1}{3}.\frac{a\sqrt{6}}{3}.\frac{1}{2}.a.\frac{a\sqrt{3}}{2}=...\)

Câu 2:

Mặt bên là tam giác cân có 1 góc bằng \(60^0\Rightarrow\) các mặt bên là các tam giác đều \(\Rightarrow SA=SB=SC=SD=AB\)

Gọi O là tâm đáy \(\Rightarrow SO\perp\left(ABCD\right)\Rightarrow SO=a\)

\(AC=AB\sqrt{2}\Rightarrow AO=\frac{1}{2}AC=\frac{AB\sqrt{2}}{2}\)

Áp dụng Pitago:

\(SA^2=SO^2+AO^2\Rightarrow AB^2=SO^2+\left(\frac{AB\sqrt{2}}{2}\right)^2\)

\(\Rightarrow AB^2=2SO^2=2a^2\)

\(\Rightarrow V=\frac{1}{3}SO.AB^2=\frac{1}{3}.a.2a^2=\frac{2}{3}a^3\)

Answer 2

[Nguyễn Việt Lâm]

Câu 3:

\(S_{ACD}=\frac{1}{2}AD.AB=a^2\)

\(\Rightarrow V_{S.ACD}=\frac{1}{3}SA.S_{ACD}=\frac{1}{3}a.a^2=\frac{a^3}{3}\)

\(S_{\Delta BCD}=\frac{1}{2}AB.BC=\frac{a^2}{2}\)

\(\Rightarrow V_{S.BCD}=\frac{1}{3}SA.S_{\Delta BCD}=\frac{a^3}{6}\)

//Kéo dài AB cắt CD tại E \(\Rightarrow AE=AD=2a\)

\(\Rightarrow AE=2AB\Rightarrow d\left(A;\left(SCD\right)\right)=2.d\left(B;\left(SCD\right)\right)\)

Có \(AC=a\sqrt{2}\) ; \(CD=a\sqrt{2}\Rightarrow AC^2+CD^2=AD^2\)

\(\Rightarrow AC\perp CD\)

Mà \(CD\perp SA\) (do \(SA\perp\left(ABCD\right)\))

\(\Rightarrow CD\perp\left(SAC\right)\)

Từ A kẻ \(AH\perp SC\Rightarrow CD\perp AH\) (do \(AH\in\left(SAC\right)\))

\(\Rightarrow AH\perp\left(SCD\right)\Rightarrow AH=d\left(A;\left(SCD\right)\right)\)

\(\frac{1}{AH^2}=\frac{1}{SA^2}+\frac{1}{AC^2}\Rightarrow AH=\frac{SA.AC}{\sqrt{SA^2+AC^2}}=\frac{a\sqrt{6}}{3}\)

\(\Rightarrow d\left(B;\left(SCD\right)\right)=\frac{1}{2}AH=\frac{a\sqrt{6}}{6}\)