Giải phương trình
x2 +2=2√(x3 +1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MH
13 tháng 4 2022
Đặt \(\left|x\right|=t\left(t\ge0\right)\). Ta có phương trình \(t^2-t=6\)
\(\Rightarrow t^2-t-6=0\Rightarrow t^2-3t+2t-6=0\)
\(\Rightarrow\left(t-3\right)\left(t+2\right)=0\Rightarrow\left[{}\begin{matrix}t=3\left(TM\right)\\t=-2\left(L\right)\end{matrix}\right.\)
\(\Rightarrow\left|x\right|=3\Rightarrow x=\pm3\)
PA
0
11 tháng 1 2022
\(a,x^3+x^2+x+1=0\\ \Rightarrow x^2\left(x+1\right)+\left(x+1\right)=0\\ \Rightarrow\left(x^2+1\right)\left(x+1\right)=0\\ \Rightarrow\left[{}\begin{matrix}x^2=-1\left(vô.lí\right)\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1\right\}\)
\(b,x^3+x^2-x-1=0\\ \Rightarrow x^2\left(x+1\right)-\left(x+1\right)=0\\ \Rightarrow\left(x^2-1\right)\left(x+1\right)=0\\ \Rightarrow\left(x-1\right)\left(x+1\right)^2=0\\ \Rightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-1;1\right\}\)
\(c,\left(x+1\right)^2\left(x+2\right)+\left(x+1\right)^2\left(x-2\right)=-24\\ \Rightarrow\left(x+1\right)^2\left(x+2+x-2\right)=-24\\ \Rightarrow2x\left(x^2+2x+1\right)=-24\\ \Rightarrow x^3+2x^2+x+12=0\\ \Rightarrow\left(x^3+3x^2\right)-\left(x^2+3x\right)+\left(4x+12\right)=0\\ \Rightarrow x^2\left(x+3\right)-x\left(x+3\right)+4\left(x+3\right)=0\\ \Rightarrow\left(x^2-x+4\right)\left(x+3\right)=0\\ \Rightarrow\left[{}\begin{matrix}\left(x-\dfrac{1}{2}\right)^2+\dfrac{15}{4}=0\left(vô.lí\right)\\x=-3\end{matrix}\right.\)
Vậy pt có tập nghiệm \(S=\left\{-3\right\}\)
HP
1 tháng 1 2021
\(x=0\) không là nghiệm của phương trình
Chia hai vế phương trình cho x, phương trình trở thành:
\(\left(x+\dfrac{4}{x}\right)+2-m=4\sqrt{x+\dfrac{4}{x}}\left(1\right)\)
Đặt \(x+\dfrac{4}{x}=t\left(t\ge2\right)\)
\(\left(1\right)\Leftrightarrow m=f\left(t\right)=t^2-4t+2\left(2\right)\)
Phương trình đã cho có nghiệm khi phương trình \(\left(2\right)\) có nghiệm \(t\ge2\)
\(\Leftrightarrow m\ge f\left(2\right)=-2\)
\(\Rightarrow\) có 2021 giá trị thỏa mãn yêu cầu bài toán
PT
1
CM
11 tháng 3 2019
+) Ta có; 8+x3 = (2 + x).( 4 - 2x+ x2 )
Mà 4 - 2x + x2 = (1 – 2x + x2 ) + 3 = ( 1- x)2 + 3 >0 với mọi x.
Do đó: 8 + x3 ≠ 0 ⇔ 2 + x ≠ 0 ⇔ x ≠ -2
+) Điều kiện xác định: x ≠ -2.
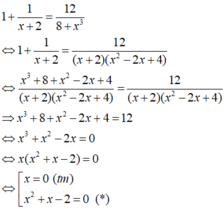
Giải phương trình (*):
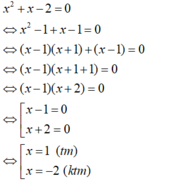
Vậy tập nghiệm của phương trình là S = {0; 1}.
28 tháng 2 2021
a. (3x - 1)2 - (x + 3)2 = 0
\(\Leftrightarrow\left(3x-1+x+3\right)\left(3x-1-x-3\right)=0\)
\(\Leftrightarrow\left(4x+2\right)\left(2x-4\right)=0\)
\(\Leftrightarrow4x+2=0\) hoặc \(2x-4=0\)
1. \(4x+2=0\Leftrightarrow4x=-2\Leftrightarrow x=-\dfrac{1}{2}\)
2. \(2x-4=0\Leftrightarrow2x=4\Leftrightarrow x=2\)
S=\(\left\{-\dfrac{1}{2};2\right\}\)
28 tháng 2 2021
b. \(x^3=\dfrac{x}{49}\)
\(\Leftrightarrow49x^3=x\)
\(\Leftrightarrow49x^3-x=0\)
\(\Leftrightarrow x\left(49x^2-1\right)=0\)
\(\Leftrightarrow x\left(7x+1\right)\left(7x-1\right)=0\)
\(\Leftrightarrow x=0\) hoặc \(7x+1=0\) hoặc \(7x-1=0\)
1. x=0
2. \(7x+1=0\Leftrightarrow7x=-1\Leftrightarrow x=-\dfrac{1}{7}\)
3. \(7x-1=0\Leftrightarrow7x=1\Leftrightarrow x=\dfrac{1}{7}\)
PT
1
CM
6 tháng 4 2017
(x – 1)(x2 + 3x – 2) – (x3 – 1) = 0
⇔ (x – 1)(x2 + 3x - 2) - (x - 1)(x2 + x + 1) = 0
⇔ (x – 1)[(x2 + 3x - 2) - (x2 + x + 1)] = 0
⇔ (x – 1). (x2 + 3x - 2 - x2 - x - 1) = 0
⇔ (x – 1)(2x - 3) = 0
⇔ x - 1 = 0 hoặc 2x - 3 = 0
+) Nếu x - 1 = 0 ⇔x = 1
+) Nếu 2x - 3 = 0 ⇔x = 3/2
Vậy tập nghiệm của phương trình là S = {1;3/2}
PT
1
\(x^2+2=2\sqrt{x^3+1}\)
\(\Rightarrow x^4+4x^2+4=4\left(x^3+1\right)\)
\(\Rightarrow x^4+4x^2+4-4x^3-4=0\)
\(\Rightarrow x^4+4x^2-4x^3=0\)
\(\Rightarrow x^2\left(x^2-4x+4\right)=0\)
\(\Rightarrow\left(x-2\right)^2=0\)
\(\Rightarrow x=2\)
\(x^2+2=2\sqrt{\left(x^3+1\right)}\)
\(\Leftrightarrow x^2+2=2\sqrt{x^3+1^3}\)
\(\Leftrightarrow x^2+2=2\sqrt{\left(x+1\right)\left[x^2-\left(x\right)\left(1\right)+1^2\right]}\)
\(\Leftrightarrow x^2+2=2\sqrt{\left(x+1\right)\left(x^2-x+1\right)}\)
\(\Leftrightarrow\left(x^2+2\right)^2=\left[2\sqrt{\left(x+1\right)\left(x^2-x+1\right)}\right]^2\)
\(\Leftrightarrow x^4+4x^2+4=4x^3-4x^2+4x+4x^2-4x+4\)
\(\Leftrightarrow x^4+4x^2=4x^3\)
\(\Leftrightarrow x^4+4x^2-4x^3=0\)
\(\Leftrightarrow x^2\left(x^2+4-4x\right)=0\)
\(\Leftrightarrow x^2\left[x^2-2\left(x\right)\left(2\right)+2^2\right]=0\)
\(\Leftrightarrow x^2\left(x-2\right)^2=0\)
\(\Leftrightarrow\orbr{\begin{cases}x=0\\x-2=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=0\\x=2\end{cases}}\)
Vậy nghiệm phương trình là: {0; 2}