Giả sử 
(a, b, m ∈ Z; m > 0) và x < y. Hãy chứng minh nếu chọn 
thì ta có x < z < y.
K
Khách
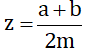
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
4
Những câu hỏi liên quan
BN
0
NA
0
CM
5 tháng 8 2017
Theo đề bài ta có 
(a, b, m ∈ Z; m > 0).
Quy đồng mẫu số các phân số ta được: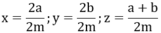 
Nhận xét: mẫu số 2m > 0 nên để so sánh x, y, z ta so sánh các tử số 2a, 2b, a+b.
Vì a < b nên a + a < b + a hay 2a < a + b.
Vì a < b nên a + b < b + b hay a + b < 2b.
Vậy ta có 2a < a+b < 2b nên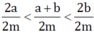 
hay x < z < y.
VH
0
CM
16 tháng 7 2019
Vì x < y nên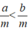 
mà m > 0 nên a < b. Ta có
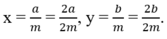
Chọn số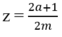 
. Do 2a < 2a + 1 và m > 0 nên 
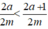hay x < z. (1)
Do a < b và a; b ∈ Z nên a + 1 ≤ b suy ra 2a + 2 ≤ 2b.
Ta có 2a + 1 < 2a + 2 ≤ 2b nên 2a + 1 < 2b, do đó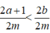 
hay z < y. (2)
Từ (1) và (2) suy ra: x < z < y
KS
2
TV
15 tháng 6 2017
Kudo Shinichi
Ta có : x < y hay a/m < b/m => a < b.
So sánh x, y, z ta chuyển chúng cùng mẫu : 2m
x = a/m = 2a/ 2m và y = b/m = 2b/2m và z = ﴾a + b﴿ / 2m
Mà : a < b
Suy ra : a + a < b + a
Hay 2a < a + b
Suy ra x < z ﴾1)
Mà : a < b
Suy ra : a + b < b + b
Hay a + b < 2b
Suy ra z < y ﴾2﴿
18 tháng 6 2017
ta có : y-x=b/m-a/m=b-a/m=b-a
mà : y>x => y-x>0(là số dương)=>b-a/m>0=>b-a>0
giả thiết đầu tiên : x<z => z-x = a+b/2m-a/m = a+b/2m-2a/2m=b-a/2m>0
=> x<z (1)
giả thiết thứ hai: z<y => y-z = b/m-a+b/2b=2b/2m-a+b/2m=b-a/2m>0
=> z<y (2)
từ (1) và (2) ta suy ra được x<z<y
BY
0
DT
0
Lẹ lên các bạn ơi
trả lời
là sao bn