a) x4+3x2-2x+1
b) x4+2x3+3x2+2x+1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
29 tháng 5 2022
3: \(x^4-13x^2+36\)
\(=x^4-9x^2-4x^2+36\)
\(=\left(x^2-9\right)\left(x^2-4\right)\)
\(=\left(x-3\right)\left(x+3\right)\left(x-2\right)\left(x+2\right)\)
4: \(x^4+3x^2-2x+3\)
\(=x^4+x^3+3x^2-x^3-x^2-3x+x^2+x+3\)
\(=\left(x^2+x+3\right)\left(x^2-x+1\right)\)
5: \(x^4+2x^3+3x^2+2x+1\)
\(=x^4+x^3+x^2+x^3+x^2+x+x^2+x+1\)
\(=\left(x^2+x+1\right)^2\)
4 tháng 1 2022
a: \(=\dfrac{x^3\left(2x-1\right)+2\left(2x-1\right)}{2x-1}=x^3+2\)
b: \(=\dfrac{2x^3-4x^2+3x^2-6x+x-2}{x-2}=2x^2+3x+1\)
d: \(=\dfrac{x^4-2x^3+3x^2+2x^3-4x^2+6x-x^2+2x-3}{x^2-2x+3}=x^2+2x-1\)
DT
7 tháng 2 2022
Đặt d : deg P(x) , ta có:
\(4=d^2\Leftrightarrow d=2\)
\(\Rightarrow P\left(x\right)=ax^2+bx+c\left(a\ne0\right)\)
Trog đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
\(x^4+2x^3+6x^2-8x+8=x^4+bx^3+\left(4+c\right).x^2+4bx+4c\)
Tiến hành đồng nhất, ta được:
\(\left\{{}\begin{matrix}b=-2\\c=2\end{matrix}\right.\)
suy ra: \(P\left(x\right)=x^2-2x+2\)
LP
7 tháng 2 2022
Đặt d : deg P(x) , ta có:
4=d2⇔d=24=d2⇔d=2
⇒P(x)=ax2+bx+c(a≠0)⇒P(x)=ax2+bx+c(a≠0)
Trong đó , hệ số cao nhất của vế trái là 1 nên a=1 . thay vào và thu gọn 2 vế đc:
x^4+2x^3+6x^2−8x+8=x^4+bx^3(4+c).x^2+4bx+4c
Tiến hành đồng nhất, ta được:
{ b=-2 c=2
suy ra: P(x)=x^2−2x+2
mình chỉ bít zậy ko biết có đúng không nữa 
CM
7 tháng 5 2019
+) Ta có
2 g ( x ) = 2 − x 4 + 2 x 3 − 3 x 2 + 4 x + 5 = − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 Ta có f ( x ) − 2 ⋅ g ( x ) = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 − − 2 x 4 + 4 x 3 − 6 x 2 + 8 x + 10 = 5 x 4 + 4 x 3 − 3 x 2 + 2 x − 1 + 2 x 4 − 4 x 3 + 6 x 2 − 8 x − 10 = 5 x 4 + 2 x 4 + 4 x 3 − 4 x 3 + − 3 x 2 + 6 x 2 + ( 2 x − 8 x ) − 1 − 1 = 7 x 4 + 3 x 2 − 6 x − 11
Hệ số cần tìm là -11
Chọn đáp án C
DX
1
31 tháng 10 2021
b: \(\dfrac{\left(x^2-1\right)\left(x^2+1\right)-2x\left(x^2-1\right)}{x^2-1}\)
\(=x^2-2x+1\)
\(=\left(x-1\right)^2\)
c: \(=\dfrac{5x^4-5x^3+14x^3-14x^2+12x^2-12x+8x-8}{x-1}\)
\(=5x^3+14x^2+12x+8\)
CM
15 tháng 3 2017
Ta có p(x) + q(x)
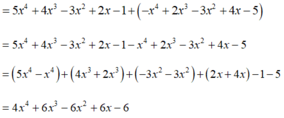
Bậc của đa thức p ( x ) + q ( x ) = 4 x 4 + 6 x 3 - 6 x 2 + 6 x - 6 l à 4
Chọn đáp án C
28 tháng 12 2021
\(1,3x-7=19\\ \Rightarrow3x=26\\ \Rightarrow x=\dfrac{26}{3}\\ 2,\left(2x+1\right)\left(x-3\right)=0\\ \Rightarrow\left[{}\begin{matrix}2x+1=0\\x-3=0\end{matrix}\right.\\ \Rightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=3\end{matrix}\right.\\ 3,3x+\dfrac{2}{4}+1=5x-\dfrac{1}{3}\\ \Rightarrow5x-\dfrac{1}{3}-3x-\dfrac{2}{4}-1=0\\ \Rightarrow2x-\dfrac{11}{6}=0\\ \Rightarrow2x=\dfrac{11}{6}\\ \Rightarrow x=\dfrac{11}{12}\)
\(4,\dfrac{x}{15}+\dfrac{1}{2}-\dfrac{x}{50}=\dfrac{5}{6}\\ \Rightarrow\dfrac{x}{15}-\dfrac{x}{50}=\dfrac{5}{6}-\dfrac{1}{2}\\ \Rightarrow x\left(\dfrac{1}{15}-\dfrac{1}{50}\right)=\dfrac{1}{3}\\ \Rightarrow\dfrac{7}{150}x=\dfrac{1}{3}\\ \Rightarrow x=\dfrac{50}{7}\)
Lâu rồi chưa làm hệ số bđ, thử nào.
b) Theo công thức ta có :
\(x^4+2x^3+3x^2+2x+1=\left(x^2+ax+b\right)\left(x^2+cx+d\right)\)
\(\Leftrightarrow x^4+2x^3+3x^2+2x+1=x^4+x^3\left(a+c\right)+x^2\left(ac+b+d\right)+x\left(ad+bc\right)+bd\)
Đồng nhất hệ số ta được :
\(\Leftrightarrow\left\{{}\begin{matrix}a+c=2\\ac+b+d=3\\ad+bc=2\\bd=1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=1\\c=1\\b=1\\d=1\end{matrix}\right.\)
Từ đó ta có : \(x^4+2x^3+3x^2+2x+1=\left(x^2+x+1\right)\left(x^2+x+1\right)\)
p/s: bài này còn một cách nữa, nếu cần thì mình chỉ thêm cho :D
fb tên là kẻ vô hình à ?