A= x\(^2\)y\(^2\) + 15x\(^2\)y - 18xy\(^2\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 11 2017
a)\(\dfrac{12x^3y^2}{18xy^5}\)=\(\dfrac{2x^2}{3y^3}\)
b)\(\dfrac{15x.\left(x+5\right)^2}{20x^2.\left(x+5\right)}\)=\(\dfrac{3.5x\left(x+5\right)}{4x.5x.\left(x+5\right)}\)=\(\dfrac{3\left(x+5\right)}{4x}\)
LH
1
10 tháng 10 2019
\(\left(y-3x\right)\left(3x+y\right)+18xy-9\left(x+y\right)^2\)
=\(\left(y-3x\right)\left(y+3x\right)+18xy-9\left(x+y\right)^2\)
\(=y^2-9x^2+18xy-9\left(x+y\right)^2\)
\(=y^2-9x^2+18xy-9\left(x^2+2xy+y^2\right)\)
\(=y^2-9x^2+18xy-9x^2-18xy-9y^2\)
\(=-8y^2\)
28 tháng 7 2017
Câu 3:
a, Ta có: \(n^2\left(n+1\right)+2n\left(n+1\right)\)
\(=\left(n^2+2n\right)\left(n+1\right)=n\left(n+1\right)\left(n+2\right)⋮6\forall n\in Z\) ( do tích của 3 số liên tiếp chia hết cho 6 )
\(\Rightarrowđpcm\)
b, \(\left(2n-1\right)^3-\left(2n-1\right)\)
\(=\left(2n-1\right)\left[\left(2n-1\right)^2-1\right]\)
\(=\left(2n-1\right)\left(2n-1-1\right)\left(2n-1+1\right)\)
\(=\left(2n-1\right)\left(2n-2\right)2n⋮8\forall n\in Z\)
\(\Rightarrowđpcm\)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 11 2019
Nhận thấy \(x=0\Rightarrow y=0\) là 1 cặp nghiệm và ngược lại
Với \(x;y\ne0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y+xy\left(x+y\right)=18xy\\x^2+y^2+x^2y^2\left(x^2+y^2\right)=208x^2y^2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+y+\frac{1}{x}+\frac{1}{y}=18\\x^2+y^2+\frac{1}{x^2}+\frac{1}{y^2}=208\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x+\frac{1}{x}+y+\frac{1}{y}=18\\\left(x+\frac{1}{x}\right)^2+\left(y+\frac{1}{y}\right)^2=212\end{matrix}\right.\)
Đặt \(\left\{{}\begin{matrix}x+\frac{1}{x}=a\\y+\frac{1}{y}=b\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}a+b=18\\a^2+b^2=212\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}a+b=18\\\left(a+b\right)^2-2ab=212\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a+b=18\\ab=56\end{matrix}\right.\)
Theo Viet đảo, a và b là nghiệm của:
\(t^2-18t+56=0\Rightarrow\left[{}\begin{matrix}t=4\\t=14\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x+\frac{1}{x}=4\\y+\frac{1}{y}=14\end{matrix}\right.\\\left\{{}\begin{matrix}x+\frac{1}{x}=14\\y+\frac{1}{y}=4\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-4x+1=0\\y^2-14y+1=0\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-14x+1=0\\y^2-4y+1=0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow...\)
14 tháng 9 2017
d)5.(x-y)-y(x-y)
=(x-y)(5-y)
e) y.(x-z)+7(z-x)
=y.(x-z)-7(x-z)
=(x-z)(y-7)
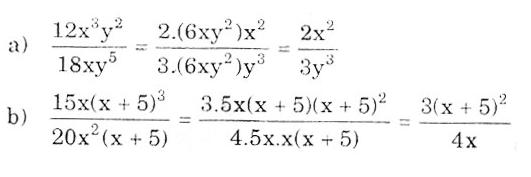
A=x2y2+15x2y-18xy2=xy(xy+15x+18y)