Chứng tỏ rằng số có dạng aabb bao giờ cx chia hết cho 11
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HV
0
MM
3
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
22 tháng 8 2020
\(\overline{aabb}=1100.a+11.b=11.\left(100.a+b\right)⋮11\)
18 tháng 9 2016
a ) aaa=a.111=a.(3.37)
=>aaa bao giờ cũng chia hết cho 37
b) aaaaaa=a.111111=a.(3.37037)
=> aaaaaa bao giờ cũng chia hết cho 3
c) abcabc=abc.1001=abc.(7.13.11)
=> abcabc bao giờ cũng chia hết cho 13;11
d) ab+ba=(10a+b)+(10b+a)=(10a+a)+(10b+b)=11a+11b
=> ab+ba chia hết cho 11
ủng hộ nha
18 tháng 9 2016
a) aaa = 111a = 37 . 3 . a
b) aaaaaa = 111111a = 37037 . 3 . a
c) abcabc = 1001abc = 77.13 . abc
abcabc = 1001abc = 77.13.abc = 7 .11.13.abc
d) (ab + ba) = 10a + b + 10b + a =11a + 11b = 11.(a+b)
12 tháng 11 2017
a) aaaaaa = a . 111111 = a .15873 . 7 = ( a . 15873 ) . 7 chia hết cho 7
Vậy aaaaaa luôc chia hết cho 7
b)abcabc = abc . 1001 = abc . 91.11=( abc . 91 ) . 11 chia hết cho 11
Vậy abcabc bao giờ cũng chia hết cho 11
TT
10
4 tháng 7 2015
abba = 1000 x a +b x 100 + 10 x b + a
abba =1001 x a + 110 x b
abba = a x 91 x 11 + b x 11 x 10
=> abba chia hết cho 11
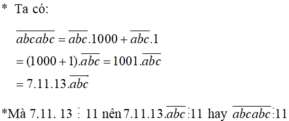
Ta có : aabb = aa00 + bb
= aa.100 + bb
= a.11.100 + b.11
= 11.(a.100 + b) \(⋮\)11
Vậy aabb \(⋮\)11 (đpcm)
Ta có : \(\overline{abab}=\overline{ab}\cdot101\)
\(\Rightarrow\overline{abab}=\overline{ab}\cdot13\cdot7\)
\(\Rightarrow\overline{abab}⋮13\)