Cho \(y=2x^2\) phải tịnh tiến ntn để được
\((P1): y = 2x^2 - 4x\)
\((P2): y=2x^2 + 6x\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TG
24 tháng 12 2021
Pt hoành độ giao điểm của (P1) và (P2) là:
\(2x^2+2x+3=x^2+6x\)
\(\Rightarrow x^2-4x+3=0\)
=> (x - 1).(x - 3) = 0
\(\Rightarrow\left[{}\begin{matrix}x_1=1\\x_2=3\end{matrix}\right.\Rightarrow\left[{}\begin{matrix}y_1=7\\y_2=27\end{matrix}\right.\)
Vậy 2 parabol này cắt nhau tại 2 điểm (1;7);(3;27)
NV
Nguyễn Việt Lâm
Giáo viên
14 tháng 9 2021
Hàm \(y=f\left(x\right)\) có đồ thị (C):
\(\Rightarrow\) Khi tịnh tiến lên a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x\right)+a\)
Khi tịnh tiến xuống dưới a đơn vị ta được đồ thị hàm \(y=f\left(x\right)-a\)
- Khi tịnh tiến sang phải a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x-a\right)\)
- Khi tịnh tiến sang trái a đơn vị sẽ được đồ thị hàm \(y=f\left(x+a\right)\)
Do đó:
Khi tịnh tiến (P) lên 4 đơn vị ta được đồ thị hàm \(y=4x^2+4\)
Khi tịnh tiến (P) sang phải 2 đơn vị ta được đồ thị hàm: \(y=4\left(x-2\right)^2=4x^2-16x+16\)
CM
1 tháng 1 2019
Ta có: M(x, y, z) ∈ (P) ⇔ d(M, ( P 1 )) = d(M, ( P 2 ))
⇔ 2|2x + y + 2z + 1| = |4x − 2y − 4z + 7|
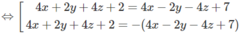
Từ đó suy ra phương trình mặt phẳng phải tìm là: 4y + 8z – 5 = 0 hoặc 8x + 9 = 0
