tìm điều kiện xác định của căn thức
\(x^2-4x+1\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài làm:
a) \(\sqrt{x^2-3x+2}=\sqrt{\left(x-1\right)\left(x-2\right)}\)
Ta xét 2 trường hợp sau:
Nếu: \(\hept{\begin{cases}x-1\ge0\\x-2\ge0\end{cases}\Rightarrow\hept{\begin{cases}x\ge1\\x\ge2\end{cases}\Rightarrow}}x\ge2\)
Nếu: \(\hept{\begin{cases}x-2\le0\\x-1\le0\end{cases}\Rightarrow}\hept{\begin{cases}x\le2\\x\le1\end{cases}\Rightarrow}x\le1\)
Vậy \(\orbr{\begin{cases}x\ge2\\x\le1\end{cases}}\)
b) \(\sqrt{2x^2+4x+5}=\sqrt{\left(x+2\right)^2+x^2+1}\)
Mà \(\left(x+2\right)^2+x^2+1>0\left(\forall x\right)\)
Vậy biểu thức xác đinh với mọi x
c) \(\sqrt{x^2+4x+5}=\sqrt{\left(x+2\right)^2+1}\)
Mà \(\left(x+2\right)^2+1>0\left(\forall x\right)\)
Vậy biểu thức xác định với mọi x
Học tốt!!!!

\(ĐK:\)
\(\sqrt{6}x-4x\ge0\)
\(\Rightarrow\left(\sqrt{6}-4\right)x\ge0\)
\(\Rightarrow x\le0\)

a: ĐKXĐ: x>=0; x<>1
b \(A=\left(\dfrac{2\sqrt{x}+x}{x\sqrt{x}-1}-\dfrac{1}{\sqrt{x}-1}\right):\dfrac{\sqrt{x}+2}{x+\sqrt{x}+1}\)
\(=\dfrac{x+2\sqrt{x}-x-\sqrt{x}-1}{x\sqrt{x}-1}\cdot\dfrac{x+\sqrt{x}+1}{\sqrt{x}+2}\)
\(=\dfrac{1}{\sqrt{x}+2}\)
c: Khi x=9-4 căn 5 thì \(A=\dfrac{1}{\sqrt{5}-2+2}=\dfrac{\sqrt{5}}{5}\)
d: căn x+2>=2
=>A<=1/2
Dấu = xảy ra khi x=0

Để phân thức xác định:
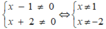
Vậy điều kiện để phân thức xác định là x ≠ -2 và x ≠ 1

đkxđ:
\(x^2-4x+3\ge0\)
\(\Leftrightarrow\left(x-1\right)\left(x-3\right)\ge0\)
\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x-1\ge0\\x-3\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}x-1\le0\\x-3\le0\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
Vậy đkxđ của biểu thức là \(\left[{}\begin{matrix}x\ge3\\x\le1\end{matrix}\right.\)
đkxđ:
�2−4�+3≥0x2−4x+3≥0
⇔(�−1)(�−3)≥0⇔(x−1)(x−3)≥0
⇔[{�−1≥0�−3≥0{�−1≤0�−3≤0⇔{x−1≥0x−3≥0{x−1≤0x−3≤0
⇔[�≥3�≤1⇔[x≥3x≤1
Vậy đkxđ của biểu thức là [�≥3�≤1[x≥3x≤1

\(a,ĐK:2-x^2\ge0\Leftrightarrow x^2\le2\Leftrightarrow-\sqrt{2}\le x\le\sqrt{2}\\ b,ĐK:5x^2-3>0\Leftrightarrow x^2>\dfrac{3}{5}\Leftrightarrow\left[{}\begin{matrix}x>\dfrac{\sqrt{15}}{5}\\x< -\dfrac{\sqrt{15}}{5}\end{matrix}\right.\\ c,ĐK:-\left(2x-1\right)^2\ge0\Leftrightarrow x=\dfrac{1}{2}\\ d,ĐK:x^2+x-2>0\\ \Leftrightarrow\left(x-1\right)\left(x+2\right)>0\\ \Leftrightarrow\left[{}\begin{matrix}x>1\\x< -2\end{matrix}\right.\)

a: ĐKXĐ: x>=0; x<>1
\(A=\dfrac{x\sqrt{x}+1}{x-1}-\dfrac{x-1}{\sqrt{x}+1}\)
\(=\dfrac{x\sqrt{x}+1-\left(x-1\right)\left(\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{x\sqrt{x}+1-x\sqrt{x}+x+\sqrt{x}-1}{x-1}=\dfrac{x+\sqrt{x}}{x-1}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-1}\)
b: Khi x=9/4 thì A=3/2:1/2=3/2*2=3