Cho góc nhọn a. Tính giá trị biểu thức \(A=\left(sinx+cosx\right)^2+\left(sinx-cosx\right)^2\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: A=(sinx+cosx)^2-1=m^2-1
b: B=căn (sinx+cosx)^2-4sinxcosx=căn m^2-4(m^2-1)=căn -3m^2+4
c: C=(sin^2x+cos^2x)^2-2(sinx*cosx)^2=1-2m^2

\(\sin x\cdot\cos x=\left(\sin x+\cos x\right)^2-\sin^2x-\cos^2x=m^2-1\)
\(A=\left|\sin x-\cos x\right|=\sqrt{\left(\sin x+\cos x\right)^2-4\sin x\cos x}\)
\(=\sqrt{m^2-4\cdot\left(m^2-1\right)}=\sqrt{m^2-4m^2+4}=\sqrt{4-3m^2}\)

\(A=\frac{sin^2x+cos^2x+2sinx.cosx-1}{\frac{cosx}{sinx}-sinx.cosx}=\frac{2sinx^2x.cosx}{cosx-sin^2x.cosx}=\frac{2sin^2x.cosx}{cosx\left(1-sin^2x\right)}\)
\(=\frac{2sin^2x}{1-sin^2x}=\frac{2sin^2x}{cos^2x}=2tan^2x\)
\(N=\left(\frac{sinx+\frac{sinx}{cosx}}{cosx+1}\right)^2+1=\left(\frac{sinx.cosx+sinx}{cosx\left(cosx+1\right)}\right)^2+1\)
\(=\left(\frac{sinx\left(cosx+1\right)}{cosx\left(cosx+1\right)}\right)^2+1=tan^2x+1=\frac{1}{cos^2x}\)

đề bài đầy đủ: rút gọn các biểu thức lượng giác sau trên điều kiện xác định của chúng:
\(\frac{sin^2x}{cosx+cosx.\frac{sinx}{cosx}}-\frac{cos^2x}{sinx+sinx.\frac{cosx}{sinx}}=\frac{sin^2x}{sinx+cosx}-\frac{cos^2x}{sinx+cosx}=\frac{sin^2x-cos^2x}{sinx+cosx}\)
\(=\frac{\left(sinx+cosx\right)\left(sinx-cosx\right)}{sinx+cosx}=sinx-cosx\)
\(\left(\frac{sinx}{cosx}+\frac{cosx}{1+sinx}\right)\left(\frac{cosx}{sinx}+\frac{sinx}{1+cosx}\right)=\left(\frac{sinx+sin^2x+cos^2x}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+cos^2x+sin^2x}{sinx\left(1+cosx\right)}\right)\)
\(=\left(\frac{sinx+1}{cosx\left(1+sinx\right)}\right)\left(\frac{cosx+1}{sinx\left(1+cosx\right)}\right)=\frac{1}{sinx.cosx}\)

\(VT=\frac{1-cosx}{sinx}\left[\frac{\left(1+cosx\right)^2}{sin^2x}-1\right]\)
\(=\frac{1-cosx}{sinx}.\left[\frac{2\left(1+cosx\right)-sin^2x}{sin^2x}-1\right]\)
\(=\frac{2\left(1-cos^2x\right)}{sin^3x}-\frac{2\left(1-cosx\right)}{sinx}\)
\(=\frac{2}{sinx}-\frac{2-2cosx}{sinx}\)
\(=\frac{2cosx}{sinx}=2cotx\)
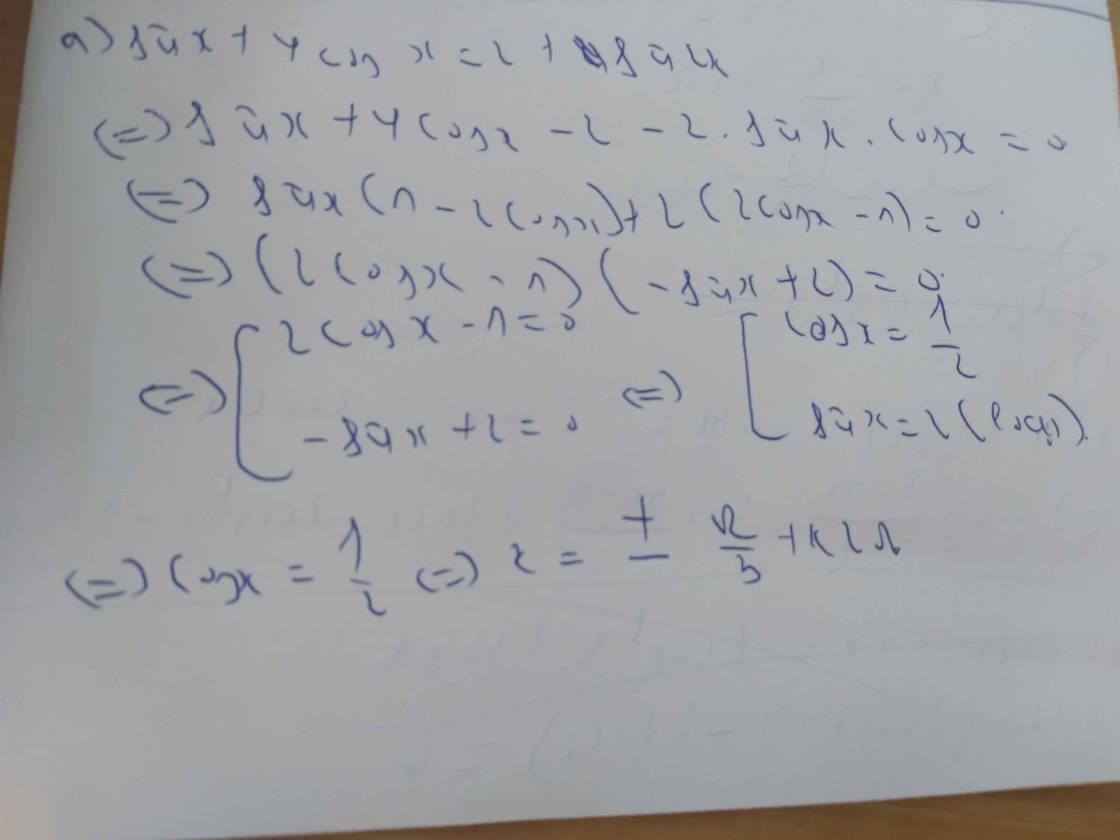

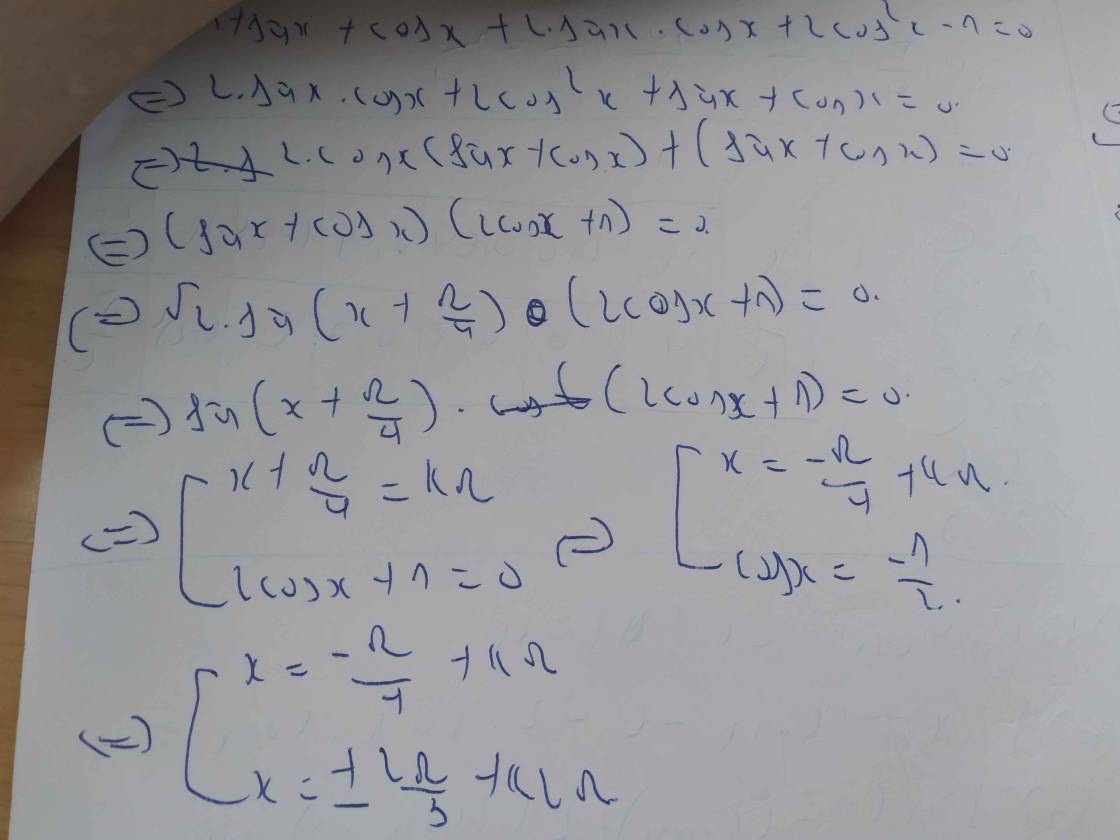



Cho góc nhọn a mà biểu thức ghi x thì hơi lạ nha =))
(Mình giải theo biểu thức nha)
\(A=\left(\sin x+\cos x\right)^2+\left(\sin x-\cos x\right)^2\\ =\sin^2x+2\sin x\cdot\cos x+\cos^2x+\sin^2x-2\sin x\cdot\cos x+\cos^2x\\ =2\sin^2x+2\cos^2x\\ =2\left(\sin^2x+\cos^2x\right)\\ =2\cdot1=2\)