B1: Cho tam giác ABC ; tia phân góc B cắt AC tại D . Tính ADB
Giúp mình với ! Thanks trước^^
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
22 tháng 9 2021
Ta có: \(\widehat{A}-\widehat{B}=\widehat{B}-\widehat{C}=10^0\)
\(\Rightarrow\widehat{A}+\widehat{C}=2\widehat{B}\)
\(\Rightarrow\widehat{A}+\widehat{B}+\widehat{C}=2\widehat{B}+\widehat{B}\)
\(\Rightarrow3\widehat{B}=180^0\Rightarrow\widehat{B}=60^0\)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{A}=10^0+\widehat{B}=70^0\\\widehat{C}=\widehat{B}-10^0=50^0\end{matrix}\right.\)
CM
12 tháng 10 2018
Đáp án C
Trọng tâm tam giác ABC là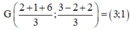 
Phép tịnh tiến T B C → biến trọng tâm G của tam giác ABC thành trọng tâm của tam giác A’B’C’, ta có
28 tháng 7 2023
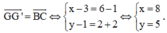
a: Xét ΔAEC và ΔAFB có
AE=AF
góc EAC chung
AC=AB
=>ΔAEC=ΔAFB
b: AE+EB=AB
AF+FC=AC
mà AE=AF và AB=AC
nên EB=FC
Xét ΔEBC và ΔFCB có
EB=FC
góc EBC=góc FCB
BC chung
=>ΔEBC=ΔFCB
10 tháng 1 2022
Sửa đề: Đường chéo AE,BD
Xét ΔAEC vuông tại E và ΔBDC vuông tại D có
góc C chung
Do đó: ΔAEC\(\sim\)ΔBDC
=>AC/BC=AE/BD=CE/CD
hay AC/CE=BC/CD
Xét ΔABC và ΔCED có
AC/CD=BC/CD
\(\widehat{C}\) chung
Do đó: ΔABC\(\sim\)ΔCED
12 tháng 1 2024
Bài 2:
\(\dfrac{S_{ABM}}{S_{ABC}}=\dfrac{8}{12}=\dfrac{2}{3}\)
=>\(\dfrac{BM}{BC}=\dfrac{2}{3}\)
=>\(BM=\dfrac{2}{3}\cdot BC=\dfrac{2}{3}\cdot24=16\left(cm\right)\)
Ta có: BM+MC=BC
=>MC+16=24
=>MC=8(cm)
(Bạn tự vẽ hình nhé !)
Vì tia phân góc B cắt AC tại D \(\Rightarrow BD\perp AC\)
\(\Rightarrow\widehat{ADB}=90^o\)