(2x+1)4=-27(2x+1)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 4 2019
Em cộng vế theo vế ta có:
\(2x^4+\left(1-2x\right)^4+2y^4+\left(1-2y\right)^4=\frac{2}{27}\)
Áp dụng BĐT cauchy schwarz dạng engel
\(2x^4+\left(1-2x\right)^4=\frac{\left(x^2\right)^2}{1}+\frac{\left(x^2\right)^2}{1}+\frac{\left(\left(1-2x\right)^2\right)^2}{1}\ge\frac{\left(x^2+x^2+\left(1-2x\right)^2\right)^2}{1+1+1}\)
\(x^2+x^2+\left(1-2x\right)^2=\frac{x^2}{1}+\frac{x^2}{1}+\frac{\left(1-2x\right)^2}{1}\ge\frac{\left(x+x+1-2x\right)^2}{1+1+1}=\frac{1}{3}\)
=> \(2x^4+\left(1-2x\right)^4\ge\frac{1}{27}\)
Tương tự \(2y^4+\left(1-2y\right)^4\ge\frac{1}{27}\)
Do đó \(2x^4+\left(1-2x\right)^4+2y^4+\left(1-2y\right)^4\ge\frac{2}{27}\)
Dấu "=" xảy ra <=> x=1-2x và y=1-2y <=> x=y=1/3
NH
2
24 tháng 3 2020
\(1+\frac{2x}{x+4}+\frac{27}{2x^2+7x-4}=\frac{6}{2x-1}\left(x\ne-4;x\ne\frac{1}{2}\right)\)
\(\Leftrightarrow1+\frac{2x}{x+4}+\frac{27}{\left(x+4\right)\left(2x-1\right)}-\frac{6}{2x-1}=0\)
\(\Leftrightarrow\frac{2x^2+7x-4}{\left(x+4\right)\left(2x-1\right)}+\frac{2x\left(2x-1\right)}{\left(x+4\right)\left(2x-1\right)}+\frac{27}{\left(x+4\right)\left(2x-1\right)}-\frac{6\left(x+4\right)}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow\frac{2x^2+7x-4}{\left(x+4\right)\left(2x-1\right)}+\frac{4x^2-2x}{\left(x+4\right)\left(2x-1\right)}+\frac{27}{\left(x+4\right)\left(2x-1\right)}-\frac{6x+24}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow\frac{2x^2+7x-4+4x^2-2x+27-6x-24}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow\frac{6x^2-x-1}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow6x^2-x-1=0\)
\(\Leftrightarrow6x^2+2x-3x-1=0\)
<=> 2x(3x+1)-(3x+1)=0
<=> (3x+1)(2x-1)=0
\(\Leftrightarrow\orbr{\begin{cases}3x+1=0\\2x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=\frac{-1}{3}\left(tm\right)\\x=\frac{1}{2}\left(ktm\right)\end{cases}}}\)
Vậy pt có nghiệm \(x=\frac{-1}{3}\)
24 tháng 3 2020
\(ĐKXĐ:x\ne-4;x\ne\frac{1}{2}\)
\(1+\frac{2x}{x+4}+\frac{27}{2x^2+7x-4}=\frac{6}{2x-1}\)
\(\Leftrightarrow\frac{\left(x+4\right)\left(2x-1\right)}{\left(x+4\right)\left(2x-1\right)}+\frac{2x\left(2x-1\right)}{\left(x+4\right)\left(2x-1\right)}+\frac{27}{\left(x+4\right)\left(2x-1\right)}-\frac{6\left(x+4\right)}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow\frac{2x^2+7x-4+4x^2-2x+27-6x-24}{\left(x+4\right)\left(2x-1\right)}=0\)
\(\Leftrightarrow6x^2-x-1=0\)
\(\Leftrightarrow\left(2x-1\right)\left(3x+1\right)=0\)
\(\Leftrightarrow x=-\frac{1}{3}\)
MH
1
NV
Nguyễn Việt Lâm
Giáo viên
9 tháng 11 2019
ĐKXĐ: \(-\frac{5}{2}\le x\le2\)
Ta có \(VT=27\left(\sqrt{5+2x}+\sqrt{4-2x}\right)\ge27\sqrt{5+2x+4-2x}=81\)
Xét vế phải với hàm \(f\left(x\right)=\left(4x+1\right)^2\) trên \(\left[-\frac{5}{2};2\right]\)
\(f\left(-\frac{1}{4}\right)=0\) ; \(f\left(-\frac{5}{2}\right)=81\) ; \(f\left(2\right)=81\)
\(\Rightarrow0\le f\left(x\right)\le81\Rightarrow VP\le81\)
\(\Rightarrow VT\ge VP\) \(\forall x\in\left[-\frac{5}{2};2\right]\)
Vậy nghiệm của BPT là \(-\frac{5}{2}\le x\le2\)
11 tháng 7 2021
9) Ta có: \(\dfrac{2x+5}{x+3}+1=\dfrac{4}{x^2+2x-3}-\dfrac{3x-1}{1-x}\)
\(\Leftrightarrow\left(2x+5\right)\left(x-1\right)+x^2+2x-3=4+\left(3x-1\right)\left(x+3\right)\)
\(\Leftrightarrow2x^2-2x+5x-5+x^2+2x-3-4-3x^2-10x+x+3=0\)
\(\Leftrightarrow-4x=9\)
hay \(x=-\dfrac{9}{4}\)
11 tháng 7 2021
10) Ta có: \(\dfrac{x-1}{x+3}-\dfrac{x}{x-3}=\dfrac{7x-3}{9-x^2}\)
\(\Leftrightarrow\dfrac{\left(x-1\right)\left(x-3\right)}{\left(x+3\right)\left(x-3\right)}-\dfrac{x\left(x+3\right)}{\left(x-3\right)\left(x+3\right)}=\dfrac{3-7x}{\left(x-3\right)\left(x+3\right)}\)
Suy ra: \(x^2-4x+3-x^2-3x-3+7x=0\)
\(\Leftrightarrow0x=0\)(luôn đúng)
Vậy: S={x|\(x\notin\left\{3;-3\right\}\)}
11) Ta có: \(\dfrac{5+9x}{x^2-16}=\dfrac{2x-1}{x+4}+\dfrac{3x-1}{x-4}\)
\(\Leftrightarrow\dfrac{\left(2x-1\right)\left(x-4\right)}{\left(x-4\right)\left(x+4\right)}+\dfrac{\left(3x-1\right)\left(x+4\right)}{\left(x-4\right)\left(x+4\right)}=\dfrac{9x+5}{\left(x-4\right)\left(x+5\right)}\)
Suy ra: \(2x^2-9x+4+3x^2+12x-x-4-9x-5=0\)
\(\Leftrightarrow5x^2-7x=0\)
\(\Leftrightarrow x\left(5x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{7}{5}\end{matrix}\right.\)
12) Ta có: \(\dfrac{2x}{2x-1}+\dfrac{x}{2x+1}=1+\dfrac{4}{\left(2x-1\right)\left(2x+1\right)}\)
\(\Leftrightarrow\dfrac{2x\left(2x+1\right)}{\left(2x-1\right)\left(2x+1\right)}+\dfrac{x\left(2x-1\right)}{\left(2x+1\right)\left(2x-1\right)}=\dfrac{4x^2-1+4}{\left(2x-1\right)\left(2x+1\right)}\)
Suy ra: \(4x^2+2x+2x^2-x-4x^2-3=0\)
\(\Leftrightarrow2x^2+x-3=0\)
\(\Leftrightarrow2x^2+3x-2x-3=0\)
\(\Leftrightarrow\left(2x+3\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{3}{2}\\x=1\end{matrix}\right.\)
CM
10 tháng 2 2018
a) 2(x + 3)(x – 4) = (2x – 1)(x + 2) – 27
⇔ 2(x2 – 4x + 3x – 12) = 2x2 + 4x – x – 2 – 27
⇔ 2x2 – 2x – 24 = 2x2 + 3x – 29
⇔ -2x – 3x = 24 – 29
⇔ - 5x = - 5 ⇔ x = -5/-5 ⇔ x = 1
Tập nghiệm của phương trình : S = {1}
b) x2 – 4 – (x + 5)(2 – x) = 0
⇔ x2 – 4 + (x + 5)(x – 2) = 0 ⇔ (x – 2)(x + 2 + x + 5) = 0
⇔ (x – 2)(2x + 7) = 0 ⇔ x – 2 = 0 hoặc 2x + 7 = 0
⇔ x = 2 hoặc x = -7/2
Tập nghiệm của phương trình: S = {2; -7/2 }
c) ĐKXĐ : x – 2 ≠ 0 và x + 2 ≠ 0 (khi đó : x2 – 4 = (x – 2)(x + 2) ≠ 0)
⇔ x ≠ 2 và x ≠ -2
Quy đồng mẫu thức hai vế :
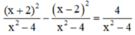
Khử mẫu, ta được : x2 + 4x + 4 – x2 + 4x – 4 = 4
⇔ 8x = 4 ⇔ x = 1/2( thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = {1/2}
d) ĐKXĐ : x – 1 ≠ 0 và x + 3 ≠ 0 (khi đó : x2 + 2x – 3 = (x – 1)(x + 3) ≠ 0)
⇔ x ≠ 1 và x ≠ -3
Quy đồng mẫu thức hai vế :
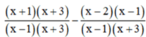
Khử mẫu, ta được : x2 + 3x + x + 3 – x2 + x – 2x + 2 + 4 = 0
⇔ 3x = -9 ⇔ x = -3 (không thỏa mãn ĐKXĐ)
Tập nghiệm của phương trình : S = ∅
PN
15 tháng 5 2021
\(2\left(x+3\right)\left(x-4\right)=\left(2x-1\right)\left(x+2\right)-27\)
\(< =>2\left(x^2-x-12\right)=2x^2+3x-2-27\)
\(< =>2x^2-2x-24=2x^2+3x-2-27\)
\(< =>5x=-24+29=5\)
\(< =>x=\frac{5}{5}=1\)
NN
3
25 tháng 9 2021
a) \(\Rightarrow2^x=32\Rightarrow2^x=2^5\Rightarrow x=5\)
b) \(\Rightarrow\left(2x+1\right)^3=5^3\)
\(\Rightarrow2x+1=5\Rightarrow x=2\)
c) \(\Rightarrow2^x=32\Rightarrow x=5\)
d) \(\Rightarrow4^3.4^x=4^5\Rightarrow4^x=4^2\Rightarrow x=2\)
e) \(\Rightarrow3^3.3^x=3^5\Rightarrow3^x=3^2\Rightarrow x=2\)
f) \(\Rightarrow7^2.7^x=7^4\Rightarrow7^x=7^2\Rightarrow x=2\)
HP
25 tháng 9 2021
a. 2x . 4 = 128
<=> 2x + 2 = 27
<=> x + 2 = 7
<=> x = 5
b. (2x + 1)3 = 125
<=> (2x + 1)3 - 53 = 0
<=> (2x + 1 - 5)\(\left[\left(2x+1\right)^2+\left(2x+1\right).5+25\right]=0\)
<=> (2x - 4)(4x2 + 4x + 1 + 10x + 5 + 25) = 0
<=> (2x - 4)(4x2 + 14x + 31) = 0
<=> \(\left[{}\begin{matrix}2x-4=0\\4x^2+14x+31=0\end{matrix}\right.\)
<=> \(\left[{}\begin{matrix}x=2\\VôNghiệm\end{matrix}\right.\)
c. 2x - 26 = 6
<=> 2x = 32
<=> x = 5
d. 64 . 4x = 45
<=> 43 . 4x = 45
<=> 43 + x = 45
<=> 3 + x = 5
<=> x = 2
e. 27 . 3x = 243
<=> 33 . 3x = 35
<=> 33 + x = 35
<=> 3 + x = 5
<=> x = 2
g. 49 . 7x = 2401 (Bn xem lại đề câu này)
<=> 72 . 7x = 74
<=> 72 + x = 74
<=> 2 + x = 4
<=> x = 2