cho tam giác ABC có góc A= 100 độ . Trên tia đối của tia BA lấy điểm D sao cho AD=BC. Tính góc ADC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


A B C D M H ve tam giac BCM deu va goi M la giao diem cua AM va BC =>BM=CM =>M nam tren duong trung truc cua BC (1) lai co tam giac ABC can => AB=AC => H nam tren duong trung truc BC (2) tu (1) va (2) =>. AM la tia phan giac => goc BAH= gocCAH =goc A /2=100/2=50 xet ABC co goc B =goc C =180-gocA /2 =180-100/2=40 ta co goc MCA = goc ACH +goc HCM <=> MCA=40+60 =100 (vi BCM la tam giac deu nen goc HCM = 60 ) vi AM la duong trung truc nen AM vuong goc BC => tam giac HMC vuong tai H => goc AMC+ goc HCM =90 <=> goc AMC +60 =90 => goc AMC =30 Xet tam giac AMC va tam giac CDA co AC chung goc A=goc C =100 CM =DA ( cung bang BC) => tam giac AMC =tam giac CDA (c.g.c) => goc AMC =goc ADC (2 goc tuong ung ) => goc ADC =30 (dpcm)
tu oanh cho mik hỏi tại sao bn lại nghĩ đến việc vẽ tam giác đều BCM vậy

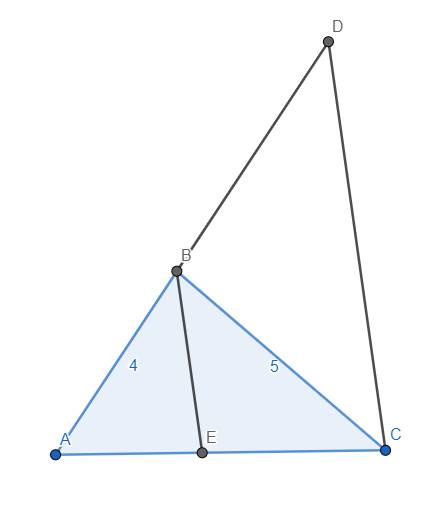
a) Xét tam giác ACB và ADC, có \(\widehat{A}\) chung và \(\widehat{ACB}=\widehat{ADC}\left(gt\right)\), suy ra đpcm.
b) Từ câu a) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AC}{AD}\) \(\Rightarrow AC^2=AB.AD\)
Kẻ phân giác BE của tam giác ABC. Vì \(\widehat{B}=2\widehat{C}\) nên \(\widehat{ABE}=\widehat{ADC}\) hay BE//CD. Mặt khác, \(\dfrac{EA}{EC}=\dfrac{BA}{BC}=\dfrac{4}{5}\) nên suy ra \(\dfrac{BA}{BD}=\dfrac{4}{5}\Leftrightarrow\dfrac{4}{BD}=\dfrac{4}{5}\Leftrightarrow BD=5\), suy ra \(AD=AB+BD=4+5=9\).
\(\Rightarrow AC^2=AB.AD=4.9=36\) \(\Rightarrow AC=6\).
Vậy \(AC=6\)
Dạ thưa cô, cái này em áp dụng tính chất đường phân giác trong tam giác ạ. Cái này lớp 9 được dùng luôn không cần chứng minh ạ.

Bài 5:
Tgiac ABC vuông cân tại A => góc CBA = 45 độ
Xét góc CBA là góc ngoài tgiac DBC => góc CBA = góc D + DCB
Xét tgiac DBC có DB = BC => tgiac DBC cân tại B => góc D = góc DBC
=> góc D = 45/2 = 22,5 độ
và góc ACD = 22,5 + 45 = 67,5 độ
Vậy số đo các góc của tgiac ACD là ...
Bài 6:
Tgiac ABC cân tại B, góc B = 100 độ => góc A = góc C = 40 độ
Xét tgiac ABD có AB = AD => tgiac ABD cân tại A => góc EDB (ADB) = (180-40)/2 =70 độ
cmtt với tgiac CBE => góc DEB = 70 độ
=> góc DBE = 180-70-70 = 40 độ
Bài 7:
Xét tgiac ABC cân tại A => góc BAC = 180 - 2.góc C => 2.(90 - góc C)
Xét tgiac BHC vuông tại H => góc CBH = 90 - góc C
=> đpcm
Bài 8: mai làm hihi