Rút gọn biểu thức: (a+b)^3+ (b+c)^3+ (c+a)^3-3(a+b)(b+c)(c+a)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2015
bài 1 : a +b , rút gọn và tính
(-a+b-c)-(a-b-c)= -a+b -c-a+b+c= -2a+2b= -2.1+2.-1=-2+-2 = -4
ST
1
27 tháng 12 2020
a) (b-c)-(b+a-c)
= b-c-b-a+c
= (b-b)-(c-c)+a
= 0 - 0 +a
= a
b) (a-b)-(-b+a-c)
=a-b-b-a+c
=(a-a)-(b-b)+c
=0 - 0 +c
=c
c) (a+b)-(a-b)+(a-c)-(a+c)
= a+b- a+b +a-c - a-c
= 0 + 0
=0
(chắc vậy
)
14 tháng 1 2017
\(A=\left(a+b-c\right)+\left(a-b\right)-\left(a-b-c\right)\)
\(=a+b-c+a-b-a+b+c\)
\(=a+b\)
\(B=\left(a-b\right)-\left(b+c\right)+\left(c-a\right)-\left(a-b-c\right)\)
\(=a-b-b-c+c-a-a+b+c\)
\(=-a-b+c\)
15 tháng 6 2021
\(A=\dfrac{x-9}{3+\sqrt{x}}\) (đề như này pk?)
a) Để A có nghĩa \(\Leftrightarrow\left\{{}\begin{matrix}x\ge0\\3+\sqrt{x}\ne0\left(lđ\right)\end{matrix}\right.\)\(\Rightarrow x\ge0\)
b) \(A=\dfrac{x-9}{3+\sqrt{x}}=\dfrac{\left(\sqrt{x}+3\right)\left(\sqrt{x}-3\right)}{3+\sqrt{x}}=\sqrt{x}-3\)
c) Với x=0 (tmđk) thay vào A ta được: \(A=\sqrt{0}-3=-3\)
Với x=-1 (ktm đk)
Với x=16 (tmđk) thay vào A ta được: \(A=\sqrt{16}-3=1\)
d) \(A\in Z\Leftrightarrow\sqrt{x}-3\in Z\Leftrightarrow\sqrt{x}\in Z\) \(\Leftrightarrow\) x là số chính phương
PK
15 tháng 1 2023
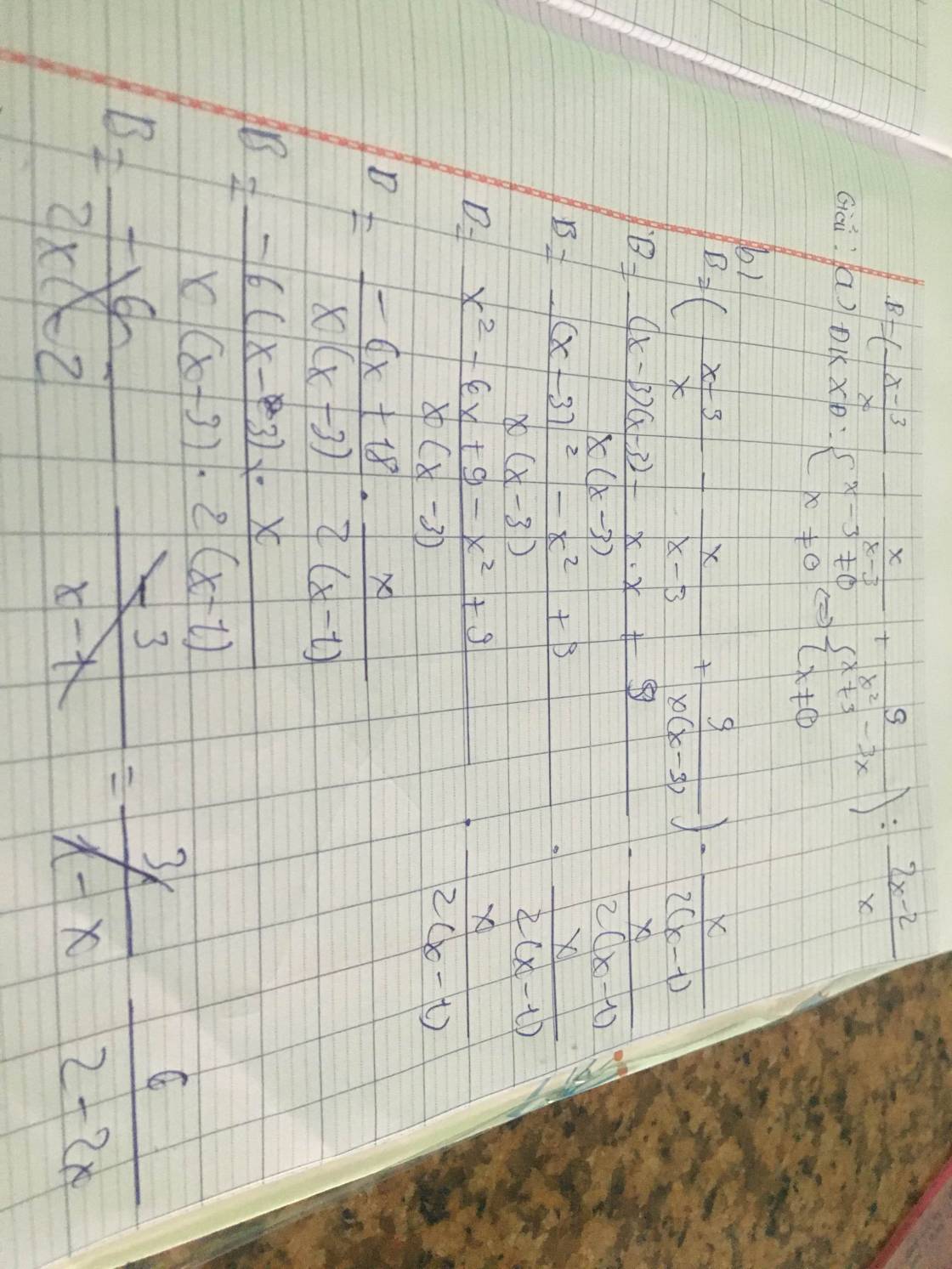c/
Ta có : B=2=>6/2-2x
<=>6=4-4x
<=>6-4=-4x
<=>-4x=2
<=>x=2/-4=-1/2
d/ĐKXĐ:2-2x≠0
<=>2(1-x)≠0<=>-2(x-1)≠0
<=>x≠1
Để giá trị của biểu thức B nguyên thì 2-2x là Ư(6)
=>2-2x ∈ Ư(6)={±1;±2;±3;±6) Nếu 2-2x=1=> -2x=-1=>x=1/2( thoả mãng)
Rồi còn nhiêu bạn tự xét trường hợp y trang cách làm ở trênn nnhan :;)).À sẽ có mấy cái trường hợp nó giống ĐKXĐ thì bạn ghi trong ngoặc ko thoã mãn nhan.
27 tháng 1 2017
A = ( - a - b + c ) - ( - a - b - c )
= - a - b + c + a + b + c
= 2c
Vậy A = 2c
k mk nha
bài đầu mk làm nhầm nha
27 tháng 1 2017
A = ( - a - b + c ) - ( - a - b - c )
A = - a - b + c + a + b + c
A = 0
Vậy A = 0
k mk nha
thank you very much
(a + b)3 + (b + c)3 + (c + a)3 - 3(a + b)(b + c)(c + a)
= a3 + 3a2b + 3ab2 + b3 + b3 + 3b2c + 3ab2 + c3 + c3 + 3c2a + 3ca2 + a3 - 3ab2 - 3a2b - 6abc - 3ac2 - 3b2c - 3bc2
= 2a3 + 3ac2 - 3ac2 - 6abc + b3 + b3 + c3 + c3 + 3bc2 - 3bc2 + 3b2c - 3b2c
= 2a3 - 6abc + b3 + b3 + c3 + c3 + 3bc2 - 3bc2 + 3b2c - 3b2c
= 2a3 - 6abc + b3 + b3 + c3 + c3
= 2a3 - 6abc + 2b3 + 2c3