Nếu x:1=y:2<0 thì \(x^2+y^2=20\)thì x+y bằng bao nhiêu
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
5
1 tháng 1 2016
Ta có
\(\frac{x}{1}=\frac{y}{2}<=>y=2x\)
Mặt khác
\(x^2+y^2=20\)
<=>\(x^2+\left(2x\right)^2=20\)
<=>\(5x^2=20\)
<=>\(x^2=4\)
<=>\(x=4;-4\)
Nếu thấy bài làm của mình đúng thì tick nha bạn,mình xin chân thành cảm ơn.
22 tháng 12 2021
c1: -0,162000>-0,(162)
c2: y=2
c3: y=-10
c4: thêm đk AC=BF
PN
0
Q
3
TM
5 tháng 6 2016
Ta có:\(\frac{x}{1}=\frac{y}{2}=\frac{x^2}{1}=\frac{y^2}{4}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có:
\(\frac{x}{1}=\frac{y}{2}=\frac{x^2}{1}=\frac{y^2}{4}=\frac{x^2+y^2}{1+4}=\frac{20}{5}=4\)
\(\Rightarrow\hept{\begin{cases}x=4.1=4\\y=4.2=8\end{cases}}\)
Vậy x+y=4+8=12
5 tháng 6 2016
Ta có : x^2 + y^2 = 20
1^2 + 2^2 = 5
20/5 = 4
x = 4 . 1 = 4
y = 4 . 2 = 8
x + y = 4 + 8 = 12
HT
2
22 tháng 11 2015
Bạn phantuananh trả lời sai, Đáp số đúng là x=-2, y=-4 và x+y=-6
1 tháng 12 2016
chịu!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
+_+
NT
0
TN
2
HP
29 tháng 12 2016
áp dụng bđt cô-si: x^2+y^2 > =2xy => 20>=2xy=>xy<=10 => 1/xy >= 10
có P=1/x^2+1/y^2=(x^2+y^2)/(xy)^2 >= 20/100=1/5
=>minP=1/5 ,dấu "=" xảy ra <=> x=y=cca8n bậc 2 của 10
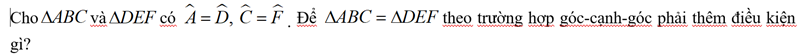
\(\frac{x}{1}=\frac{y}{2}=k<0\Leftrightarrow\frac{x^2}{1}=\frac{y^2}{4}=\frac{x^2+y^2}{1+4}=\frac{20}{5}=4=k^2\Leftrightarrow k=-2\)
x =-2
y =-4
=> x+y = -2 -4 =-6