Điền các số 1 , 2 , 3, 4, 5, 6, 7, 8, 9 vào bảng để có 1 ma phương
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
NN
Nguyễn Nhật Minh
19 tháng 6 2019
| 8 | 1 | 6 |
| 3 | 5 | 7 |
| 4 | 9 | 2 |
Đúng(0)
Những câu hỏi liên quan
GN
GV Nguyễn Trần Thành Đạt
Giáo viên
1 tháng 8 2023
Theo thứ tự đáp án nha!
1
4
9
16
25
36
49
64
81
100
121
144
169
196
225
256
289
324
361
400
1 tháng 8 2023
| 4 |
| 9 |
| 16 |
| 25 |
| 36 |
| 49 |
| 64 |
| 81 |
| 100 |
| 121 |
| 144 |
| 169 |
| 196 |
| 225 |
| 256 |
| 289 |
| 324 |
| 361 |
| 400 |
8 tháng 1 2017
mới nhìn câu đầu đã thấy tào lao
thử cho coi :
1...1...1=6
thử công trừ nhân chia nha !!!
1+1+1=3(sai)
1-1-1=-1(sai)
1x1x1=1(sai)
1:1:1=1(sai)
Thử các phép tổng hợp :
1+1-1=1(sai)
1-1+1=1(sai)
1+1x1=2(sai)
1+1:1=2(sai)
Và các phép khác cũng vậy số lớn nhất đạt được chỉ có 3 thôi !!!
MT
7 tháng 3 2017
1+1+1! = 6 7-7:7 = 6
2+2+2=6 bình phương của 10 - 10:10 sau đó giai thừa thì bằng 3!=6
3.3-3=6 bình phương của ((8:8)+8) =3 sau đó giai thừa lên thì có 3!=6
4-4:4!=6 bình phương của (9-9+9) =3 sau đó giai thừa lên thì có 3!=6
5:5+5=6
thế là ok
CM
1 tháng 8 2019
Chọn đáp án C.
Số cách sắp xếp 9 chữ số đã cho vào ô vuông bằng n(Ω)=9!
Ta có: A là biến cố: “tồn tại một hàng hoặc một cột gồm ba số chẵn”.
Do có 4 số chẵn (2, 4, 6, 8) nên A là biến cố: “có đúng một hàng hoặc một cột gồm 3 số chẵn”.
Ta tính n A :
Chọn 4 ô điền số chẵn:
Ø Chọn một hàng hoặc một cột thì có 6 cách.
Ø Chọn một ô còn lại có 6 cách.
Điền 4 số chẵn vào 4 ô trên có 4! cách.
Điền 5 số lẻ vào 5 ô còn lại có 5! Cách.
CM
29 tháng 5 2018
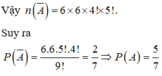
Chọn B
Ta có 
Xét A ¯ : Có ít nhất một hàng hoặc một cột chỉ toàn số chẵn.
Vì chỉ có 4 số chẵn là 2, 4, 6, 8 nên chỉ có thể có đúng một hàng hoặc đúng một cột chỉ toàn các số chẵn. Để điền như vậy cần chọn một trong số ba hàng hoặc ba cột rồi chọn 3 số chẵn xếp vào hàng hoặc cột đó, 6 số còn lại xếp tùy ý. Do đó 
Vậy 