Trên đường thẳng x'x có 1 điểm O . Trên cùng một nửa mp bờ x'x vẽ hai tia Oy , Oz sao cho xOy = x'Oz = 120^o . Trên nửa mp đối của nửa mp chứa tia Oz , bờ x'x vẽ tia Oz' sao cho x'Oz = 60^o a) Chứng tỏ 2 góc x'Oz' và xOz là 2 góc đối đỉnh b) Chứng tỏ Ox' là tia phân giác của yOz
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

b) Ta có: (d2): \(y=\dfrac{-x}{3}-\dfrac{1}{2}\)
\(\Leftrightarrow y=\dfrac{-1}{3}x-\dfrac{1}{2}\)
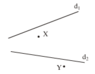
Gọi A(xA;yA) là giao điểm của (d1) và (d2)
Hoành độ của A là:
\(\dfrac{-1}{3}x-\dfrac{1}{2}=2-x\)
\(\Leftrightarrow\dfrac{-1}{3}x-\dfrac{1}{2}-2+x=0\)
\(\Leftrightarrow\dfrac{2}{3}x-\dfrac{5}{2}=0\)
\(\Leftrightarrow\dfrac{2}{3}x=\dfrac{5}{2}\)
\(\Leftrightarrow x=\dfrac{5}{2}:\dfrac{2}{3}=\dfrac{5}{2}\cdot\dfrac{3}{2}=\dfrac{15}{4}\)
Thay \(x=\dfrac{15}{4}\) vào hàm số y=2-x, ta được:
\(y=2-\dfrac{15}{4}=\dfrac{8}{4}-\dfrac{15}{4}=-\dfrac{7}{4}\)
Vậy: \(A\left(\dfrac{15}{4};-\dfrac{7}{4}\right)\)

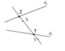
Vì X, Z, T thẳng hàng và Y, Z, T thẳng hàng nên cả 4 điểm này đều nằm trên đường thẳng XY.
Cách vẽ: Vẽ đường thẳng XY cắt d1 tại Z, cắt d2 tại T.

Vì đường thẳng y = (2m - 1)x - 3m + 7 cắt đường thẳng y = x - 1 tại điểm trên trục hoành nên tung độ bằng 0 hay y = 0.
Thay y = 0 vào pt y = x - 1 ta có :
x - 1 = 0 => x = 1
Vậy giao điểm của 2 đt là A( 1; 0)
Thay tọa độ điểm A vào pt đt y = ( 2m -1) x - 3m + 7 ta có :
(2m -1) .1 - 3m + 7 = 0
2m - 1 - 3m + 7 = 0
-m + 6 = 0
m = 6
Kết luận : với m = 6 thì đt y = (2m -1)x - 3m + 7 có dạng :
y = 11x - 11 và cắt đường thẳng y = x - 1 tại 1 điểm trên trục hoành.
Sửa đề:
Trên đường thẳng x'x có 1 điểm O . Trên cùng một nửa mp bờ x'x vẽ hai tia Oy , Oz sao cho xOy = x'Oz = 120^o . Trên nửa mp đối của nửa mp chứa tia Oz , bờ x'x vẽ tia Oz' sao cho x'Oz' = 60^o a) Chứng tỏ 2 góc x'Oz' và xOz là 2 góc đối đỉnh b) Chứng tỏ Ox' là tia phân giác của yOz'
x x' z' y z O
a)Có tia Ox nằm giữa hai tia Oz và Oz'
=>\(\widehat{x'Oz}+\widehat{x'Oz'}=\widehat{zOz'}\)
Thay số:\(120^o+60^o=\widehat{zOz'}\)
=>\(\widehat{zOz'}=180^o\)
=> zz' là đường thẳng.
Có hai đường thẳng xx' và zz' cắt nhau ở O
=>\(\widehat{xOz}=\widehat{x'Oz'}\) (hai góc đối đỉnh)
b)Ta có:
+)\(\widehat{xOy}+\widehat{x'Oy}=180^o\)
+)\(\widehat{x'Oz}+\widehat{xOz}=180^o\)
Mà \(\widehat{xOy}=\widehat{x'Oz}\) (vì \(120^o=120^o\))
=>\(\widehat{x'Oy}=\widehat{xOz}\)
Lại có: \(\widehat{xOz}=\widehat{x'Oz'}\) (câu a)
=> \(\widehat{x'Oy}=\widehat{x'Oz'}\)
=>Ox' là tia phân giác của \(\widehat{yOz'}\)