Tính \(\cos^2\) 20 độ + \(\cos^2\) 40 độ + \(\cos^2\) 50 độ + \(\cos^2\) 70 độ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KT
Tính:
a) A= cos2 20 độ + cos2 40 độ + cos2 50 độ + cos2 70 độ
b) B= sin4 a + cos4 a + 2sin2 a . cos2 a
0
NT
2
29 tháng 10 2023
a: \(cos70=sin20\)
20<25
=>\(sin20< sin25\)
=>\(cos70< sin25\)
b: \(\dfrac{sin50}{cos40}=\dfrac{cos\left(90-50\right)}{cos40}=\dfrac{cos40}{cos40}=1\)
H9
HT.Phong (9A5)
CTVHS
29 tháng 10 2023
a) Ta có:
\(cos70^o=sin\left(90^o-70^o\right)=sin20^o\)
Ta so sánh \(sin25^o\) và \(sin20^o\)
\(25^o>20^o\Rightarrow sin25^o>sin20^o\)
\(\Rightarrow sin25^o>cos70^o\)
b) \(\dfrac{sin50^o}{cos40^o}\)
Ta có:
\(cos40^o=sin\left(90^o-40^o\right)=sin50^o\)
\(\Rightarrow\dfrac{sin50^o}{cos40^o}=\dfrac{sin50^o}{sin50^o}=1\)
27 tháng 10 2023
a: 
b: \(B=3-sin^290^0+2\cdot cos^260^0-3\cdot tan^245^0\)
\(=3-1+2\cdot\left(\dfrac{1}{2}\right)^2-3\cdot1^2\)
\(=2-3+2\cdot\dfrac{1}{4}=-1+\dfrac{1}{2}=-\dfrac{1}{2}\)
c: \(C=sin^245^0-2\cdot sin^250^0+3\cdot cos^245^0-2\cdot sin^240^0+4\cdot tan55\cdot tan35\)
\(=\left(\dfrac{\sqrt{2}}{2}\right)^2+3\cdot\left(\dfrac{\sqrt{2}}{2}\right)^2-2\cdot\left(sin^250^0+sin^240^0\right)+4\)
\(=\dfrac{1}{2}+3\cdot\dfrac{1}{2}-2+4\)
\(=2-2+4=4\)
H9
HT.Phong (9A5)
CTVHS
17 tháng 8 2023
\(A=sin^210^o+cos^220^o+sin^280^o+cos^270^o\)
\(A=\left(sin^210^o+sin^280^o\right)+\left(cos^220^o+cos^270^o\right)\)
\(A=0+0\)
\(A=0\)
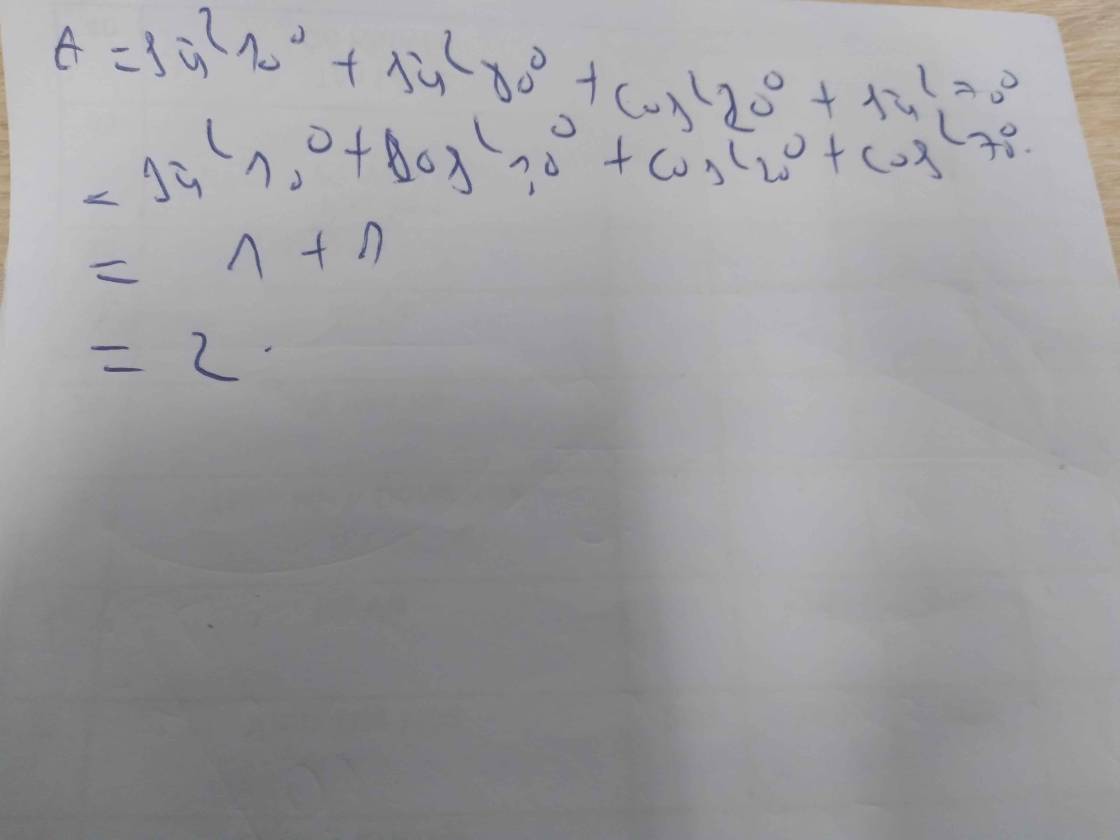
Lời giải:
Áp dụng công thức \(\left\{\begin{matrix} \cos \alpha=\sin (90-\alpha)\\ \cos ^2\alpha+\sin ^2\alpha=1\end{matrix}\right.\) ta có:
\(\cos ^220+\cos ^240+\cos ^250+\cos ^270\)
\(=\sin ^2(90-20)+\sin ^2(90-40)+\cos ^250+\cos ^270\)
\(=\sin ^270+\sin ^250+\cos ^250+\cos ^270\)
\(=(\sin ^270+\cos ^270)+(\sin ^250+\cos ^250)=1+1=2\)