Trên mặt phẳng tọa độ Oxy, cho điểm N(3;-2) và đường thẳng d có phương trình y = x-m với m là tham số.
a) Tìm m để N thuộc đường thẳng d
b) Với m tìm xác định tọa độ giao điểm của đường thẳng d và parabol (P) có phương trình y=-4x2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(\overrightarrow{AB}=\left(-3;7\right)\)
\(\overrightarrow{DC}=\left(1-x_D;5-y_D\right)\)
Để ABCD là hbh thì
\(\left\{{}\begin{matrix}1-x_D=-3\\5-y_D=7\end{matrix}\right.\Leftrightarrow D\left(2;-2\right)\)

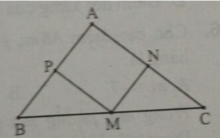
Tam giác ABC có M; N ; P lần lượt là trung điểm của BC; AC ; BC nên PM và MN là đường trung bình của tam giác ABC.
Suy ra: PM// AC; NM // AB.
Do đó, tứ giác ANMP là hình bình hành.
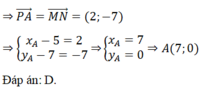

Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

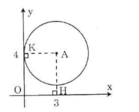
Kẻ AH ⊥ Ox, AK ⊥ Oy.
Vì AH = 4 > R = 3 nên đường tròn tâm (A) và trục hoành không giao nhau.
Vì AK = 3 = R nên đường tròn (A) và trục tung tiếp xúc nhau.

\(a,\) Thay \(x=3;y=4\Rightarrow\dfrac{4}{3}\cdot3=4\) (đúng)
Vậy \(A\left(3;4\right)\in y=\dfrac{4}{3}x\)

Tọa độ điểm I của đoạn thẳng MN là:
x I = x M + x N 2 = 0 + ( − 3 ) 2 = − 3 2 y I = y M + y N 2 = 4 + 2 2 = 3 ⇒ I − 3 2 ; 3
Đáp án C
b) Với m tìm được, xác định tọa độ giao điểm của đường thẳng d và parabol (P) có phương trình y=-4x2