vẽ hình giúp em và giải ạ

Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


+ Góc \(\widehat{AOD}\)
\(\Rightarrow\widehat{AOD}+\widehat{DOB}=\widehat{AOB}\)
\(\Rightarrow\widehat{AOD}+90^O=120^O\)
\(\Rightarrow\widehat{AOD}=120^O-90^O=30^O\)
+ Góc \(\widehat{BOC}\)
\(\Rightarrow\widehat{AOC}+\widehat{COB}=\widehat{AOB}\)
\(\Rightarrow90^O+\widehat{COB}=120^O\)
\(\Rightarrow\widehat{COB}=120^O-90^O=30^O\)
Vậy \(\widehat{AOD}=\widehat{BOC}=30^O\)
Hình vẽ :


Xét hình thang ABCD có EG//AB//CD
nên AE/AD=BG/BC
Xét ΔADC có OE//DC
nên OE/DC=AE/AD
Xét ΔBDC có OG//DC
nên OG/DC=BG/BC
=>OE/DC=OG/DC
=>OE=OG

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

a: Xét tứ giác AECF có
AE//CF
AE=CF
Do đó: AECF là hình bình hành
b: ABCD là hình chữ nhật
=>AC cắt BD tại trung điểm của mỗi đường
=>O là trung điểm chung của AC và BD
AECF là hình bình hành
=>AC cắt EF tại trung điểm của mỗi đường
mà O là trung điểm của AC
nên O là trung điểm của EF
=>E,O,F thẳng hàng
c: Nếu EF cắt BD tại K thì K trùng với O rồi bạn
Xét ΔADC có
AF,DO là trung tuyến
AF cắt DO tại I
Do đó: I là trọng tâm của ΔADC
=>IO=1/3DO
=>\(IK=\dfrac{1}{3}DK\)

10: Chọn B
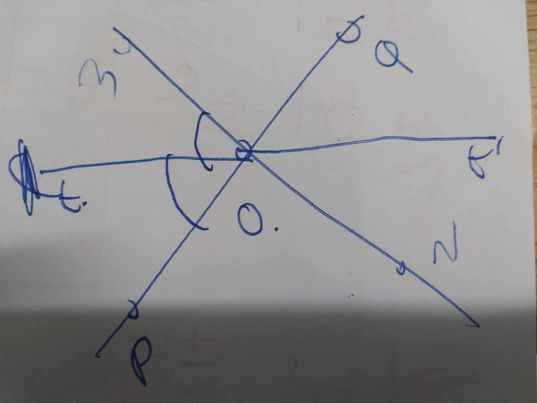
Ot là phân giác của \(\widehat{MOP}\)
=>\(\widehat{MOP}=2\cdot\widehat{tOP}\)
\(\widehat{MOP}=\widehat{NOQ}\)
=>\(\widehat{NOQ}=2\cdot\widehat{tOP}\)
mà \(\widehat{tOP}=\widehat{t'OQ}\)(hai góc đối đỉnh)
nên \(\widehat{NOQ}=2\cdot\widehat{t'OQ}\)
=>Ot' là phân giác của góc NOQ
11:
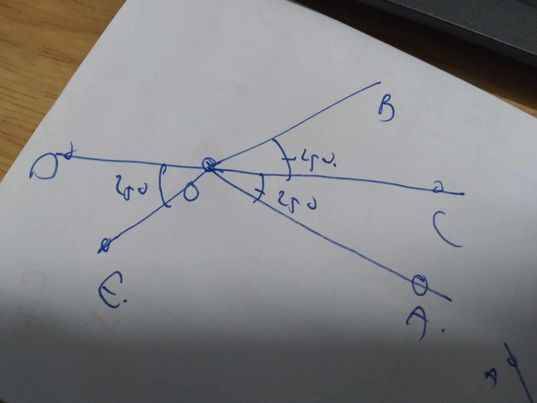
OC là phân giác của góc AOB
=>\(\widehat{AOC}=\widehat{BOC}=\dfrac{50^0}{2}=25^0\)
\(\widehat{DOE}=\widehat{BOC}\left(=25^0\right)\)
=>\(\widehat{DOE}+\widehat{DOB}=180^0\)
=>OB và OE là hai tia đối nhau
=>Hai góc đối đỉnh là \(\widehat{BOC};\widehat{DOE}\)
=>Chọn D
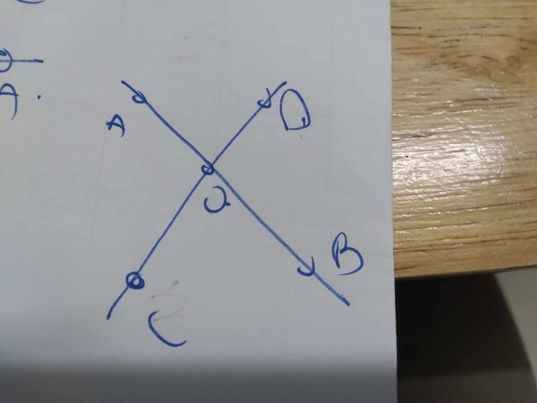
12:
\(\widehat{AOC}+\widehat{AOD}=180^0\)
\(\widehat{AOC}-\widehat{AOD}=50^0\)
Do đó: \(\widehat{AOC}=\dfrac{180^0+50^0}{2}=115^0;\widehat{AOD}=115^0-50^0=65^0\)
=>\(\widehat{BOC}=\widehat{AOD}=65^0\)
=>Chọn B


a: Xét ΔABD và ΔHBD có
BA=BH
\(\widehat{ABD}=\widehat{HBD}\)
BD chung
Do đó: ΔABD=ΔHBD
b: Ta có: ΔABD=ΔHBD
nên \(\widehat{BAD}=\widehat{BHD}\)
mà \(\widehat{BAD}=90^0\)
nên \(\widehat{BHD}=90^0\)
hay DH\(\perp\)BC

b: Xét ΔABD và ΔBAC có
BA chung
BD=AC
AD=BC
Do đó: ΔABD=ΔBAC
c: ta có: EA+EC=AC
EB+ED=BD
mà AC=BD
và EA=EB
nên EC=ED
a: Xét ΔADM và ΔCBN có
\(\widehat{ADM}=\widehat{CBN}\)
AD=BC
\(\widehat{DAM}=\widehat{BCN}\)
Do đó: ΔADM=ΔCBN
Suy ra: AM=CN