Giải phương...
Đọc tiếp
Giải phương trình:
24√x23 +4=1+√3x2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 6 2019
Đáp án B.
Ta có
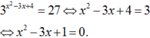
Suy ra x 1 + x 2 = 3 ; x 1 x 2 = 1 và x 1 3 + x 2 3 = ( x 1 + x 2 ) 3 - 3 x 1 x 2 ( x 1 + x 2 ) = 18
Do đó log 2 x 1 3 + x 2 3 - 2 = log 2 16 = 8
Phân tích phương án nhiễu.
Phương án A: Sai do HS tính đúng x 1 3 + x 2 3 - 2 = 16 nhưng lại tính sai log 2 x 1 3 + x 2 3 - 2 = log 2 16 = 4 .
Phương án C: Sai do HS tính sai x 1 + x 2 = - 3 nên x 1 3 + x 2 3 - 2 = - 20 Do đó log 2 x 1 3 + x 2 3 - 2 = log 2 400 .
Phương án D: Sai do HS biến đổi sai
3 x 2 - 3 x + 4 = 27 ⇔ x 2 - 3 x + 4 = 9 ⇔ x 2 - 3 x - 5 = 0
Do đó dẫn đến tính sai x 1 3 + x 2 3 - 2 = 70 .
Suy ra log 2 x 1 3 + x 2 3 - 2 = 2 + log 2 1255 .
PT
1
5 tháng 7 2019
3x2 + 2x - 1 = 0
=> 3x2 + 3x - x - 1 = 0
=> 3x(x + 1) - (x + 1) = 0
=> (3x - 1)(x + 1) = 0
=> \(\orbr{\begin{cases}3x-1=0\\x+1=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=\frac{1}{3}\\x=-1\end{cases}}\)
x2 - 5x + 6 = 0
=> x2 - 2x - 3x + 6 = 0
=> x(x - 2) - 3(x - 2) = 0
=> (x - 3)(x - 2) = 0
=> \(\orbr{\begin{cases}x-3=0\\x-2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=3\\x=2\end{cases}}\)
3x2 + 7x + 2 = 0
=> 3x2 + 6x + x + 2 = 0
=> 3x(x + 2) + (x + 2) = 0
=> (3x + 1)(x + 2) = 0
=> \(\orbr{\begin{cases}3x+1=0\\x+2=0\end{cases}}\)
=> \(\orbr{\begin{cases}x=-\frac{1}{3}\\x=-2\end{cases}}\)
5 tháng 7 2019
1, \(3x^2+2x-1=0\Leftrightarrow3x^2+3x-x-1=0\)
\(\Leftrightarrow3x\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(x+1\right)\left(3x-1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+1=0\\3x-1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-1\\x=\frac{1}{3}\end{cases}}}\)
2, \(x^2-5x+6=0\Leftrightarrow x^2-2x-3x+6=0\)
\(\Leftrightarrow x\left(x-2\right)-3\left(x-2\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x-3\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x-2=0\\x-3=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=2\\x=3\end{cases}}}\)
3, \(3x^2+7x+2=0\Leftrightarrow3x^2+6x+x+2=0\)
\(\Leftrightarrow3x\left(x+2\right)+\left(x+2\right)=0\)
\(\Leftrightarrow\left(x+2\right)\left(3x+1\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}x+2=0\\3x+1=0\end{cases}\Leftrightarrow\orbr{\begin{cases}x=-2\\x=-\frac{1}{3}\end{cases}}}\)
CM
18 tháng 10 2018
Phương trình 2 x 2 − 18x + 15 = 0 có = 61 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có
Ta có
( x 1 + x 2 ) 3 = x 1 3 + 3 x 12 x 2 + 3 x 1 x 22 + x 2 3 ⇒ ( x 1 + x 2 ) 3 = x 1 3 + x 2 3 + 3 x 1 x 2 ( x 1 + x 2 ) ⇒ x 1 3 + x 2 3 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 )
Nên
C = x 1 3 + x 2 3 = x 1 + x 2 3 - 3 x 1 x 2 ( x 1 + x 2 )
= 9 3 – 3 . 3 . 15 2 = 1053 2
Đáp án: B
CM
11 tháng 9 2017
Phương trình x 2 − 20x − 17 = 0 có = 468 > 0 nên phương trình có hai nghiệm x 1 ; x 2
Theo hệ thức Vi-ét ta có x 1 + x 2 = − b a x 1 . x 2 = c a ⇔ x 1 + x 2 = 20 x 1 . x 2 = − 17
Ta có
C = x 1 3 + x 2 3 = x 1 3 + 3 x 1 2 x 2 + 3 x 1 x 2 2 + x 2 3 − 3 x 1 2 x 2 − 3 x 1 x 2 2 = ( x 1 + x 2 ) 3 − 3 x 1 x 2 ( x 1 + x 2 ) = 2 3 – 3 . ( − 17 ) . 20 = 9020
Đáp án: D
DT
Đỗ Thanh Hải
CTVVIP
16 tháng 4 2021
1) \(\left\{{}\begin{matrix}2x+y=10\\5x-3y=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}10x+5y=50\\10x-6y=6\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}11y=44\\2x+y=10\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=4\\x=3\end{matrix}\right.\)
Vậy hpt có nghiệm (x;y) = (3;4)
2)
a) 3x2 - 2x - 1 = 0
\(\Leftrightarrow3x^2-3x+x-1=0\)
\(\Leftrightarrow3x\left(x-1\right)+\left(x-1\right)=0\)
\(\Leftrightarrow\left(3x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{3}\\x=1\end{matrix}\right.\)
Vậy pt có nghiệm x = 1 hoặc x = 3
b) Đặt x2 = t (t \(\ge\) 0)
Pt trở thành: t2 - 20t + 4 = 0
\(\Delta\) = (-20)2 - 4.1.4 = 400 - 16 = 384
=> pt có 2 nghiệm phân biệt t1 = \(\dfrac{20+8\sqrt{6}}{2}=10+4\sqrt{6}\)
t2 = \(\dfrac{20-8\sqrt{6}}{2}=10-4\sqrt{6}\)
=> x1 = \(\sqrt{10+4\sqrt{6}}=\sqrt{\left(2+\sqrt{6}\right)^2}=2+\sqrt{6}\)
x2 = \(2-\sqrt{6}\)