Tìm giá trị thực của tham số m để hàm số y=\(\frac{1}{3}\)x3-mx2+(m2-m-1)x đạt cực đại tại x=1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
5 tháng 12 2018
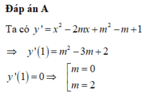
+ Với m=0 khi đó phương trình y’ = 0 sẽ có nghiệm kép nên loại.
+ Với m=2 thì khi đó phương trình y’=0 có hai nghiệm.
Chọn phương án A.
.
.
.
.
.
.
CM
15 tháng 6 2019
Đáp án C
Ta có y ' = x 2 - 2 m x + m 2 - 4 y ' ' = 2 x - 2 m .
Hàm số y = 1 3 x 3 - m x 2 + ( m 2 - 4 ) x + 3 đạt cực đại tại x=3 khi và chỉ khi
y ' ( 3 ) = 0 y ' ' ( 3 ) < 0 ⇔ m 2 - 6 m + 5 = 0 6 - 2 m < 0 ⇔ m = 1 m = 5 m > 3 .
CM
11 tháng 4 2017
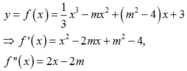
Hàm số bậc ba y = 1 3 x 3 - m x 2 + m 2 - 4 x + 3 đạt cực đại tại
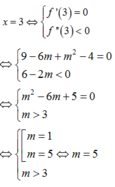
Vậy, m = 5
Chọn: B
CM
23 tháng 3 2017
Chọn B.
Đạo hàm: y’ = 3x2 – 2mx + 2m – 3 và y” = 6x – 2m
+ Để hàm số đạt cực đại x = 1 thì:
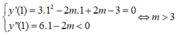
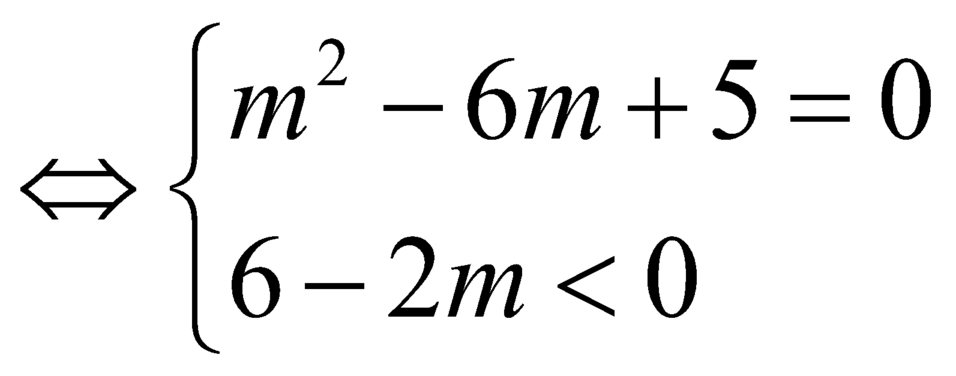
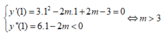
\(y'=x^2-2mx+\left(m^2-m-1\right)\) (1)
Để hàm số có cực đại cực tiểu thì (1) có 2 nghiệm phân biệt
\(\Delta'=m+1>0\Rightarrow m>-1\)
Do \(a=1>0\) nên hoành độ điểm cực đại là nghiệm nhỏ hơn của pt (1)
\(\Rightarrow m-\sqrt{m+1}=1\Rightarrow m-1=\sqrt{m+1}\)
\(\Rightarrow\left\{{}\begin{matrix}m\ge1\\\left(m-1\right)^2=m+1\end{matrix}\right.\) \(\Rightarrow m=3\)