cho hình chữ nhật ABCD. trong đó BM⊥AC tại N, BM ⊥ CD, AD tại E và F
CMR AM.AC + BM . BE = BD2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2022
a. Xét △DMI có: AB//DM.
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{IA}{IM}\) (hệ quả định lí Ta-let)
a. Xét △CMK có: AB//CM.
\(\Rightarrow\dfrac{AB}{CM}=\dfrac{KB}{KM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{AB}{DM}=\dfrac{KB}{KM}\)
-Xét △ABM có: \(\dfrac{IA}{IM}=\dfrac{KB}{KM}\left(=\dfrac{AB}{DM}\right)\)
\(\Rightarrow\)IK//AB (định lí Ta-let đảo).
b) -Xét △ADM có: EI//DM.
\(\Rightarrow\dfrac{EI}{DM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
-Xét △ACM có: KI//CM.
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{AI}{AM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{AI}{AM}=\dfrac{EI}{DM}\) nên \(IK=EI\).
-Xét △BCM có: KF//CM.
\(\Rightarrow\dfrac{KF}{CM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
-Xét △BDM có: IK//DM.
\(\Rightarrow\dfrac{IK}{DM}=\dfrac{BK}{BM}\) (hệ quả định lí Ta-let)
Mà \(DM=CM\) (M là trung điểm DC)
\(\Rightarrow\dfrac{IK}{CM}=\dfrac{BK}{BM}=\dfrac{KF}{CM}\) nên \(IK=KF\)
-Vậy \(EI=IK=KF\)
8 tháng 12 2021
1:
a: Xét tứ giác BMDN có
DM//BN
DM=BN
Do đó: BMDN là hình bình hành
Suy ra: BM//DN
24 tháng 12 2023
a: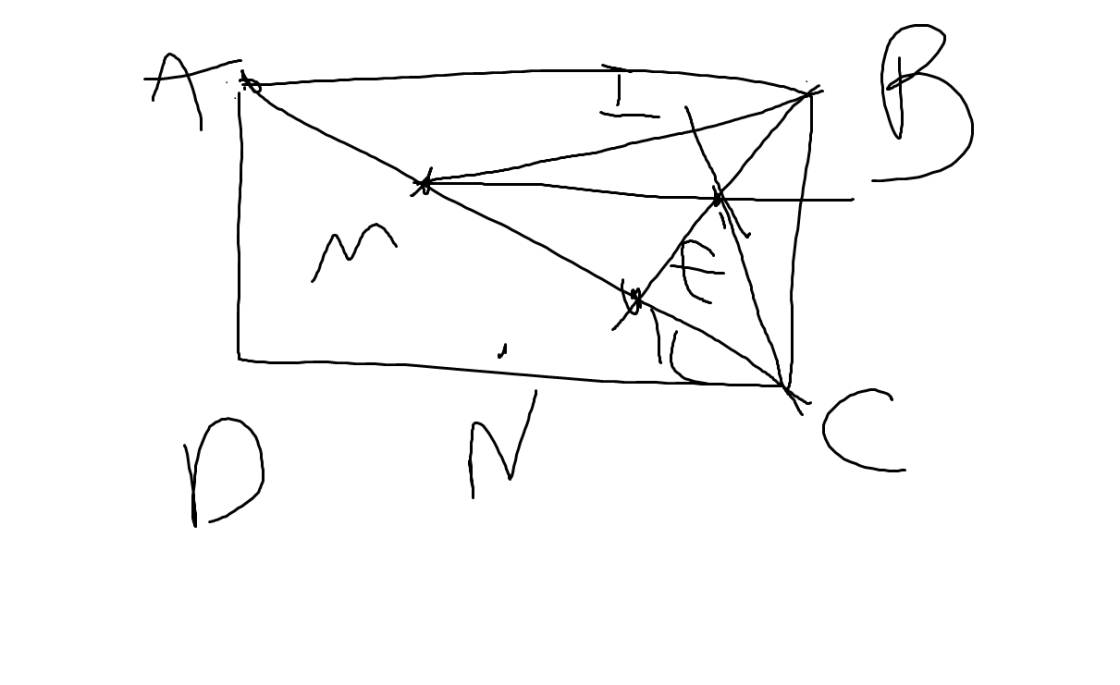 
b: Xét ΔBMC có
BK,CI là các đường cao
BK cắt CI tại E
Do đó: E là trực tâm của ΔBMC
=>ME\(\perp\)BC
mà AB\(\perp\)BC
nên ME//AB
Xét ΔKAB có
M là trung điểm của KA
ME//AB
Do đó: E là trung điểm của BK
=>BE=EK
c: Xét ΔKAB có
M,E lần lượt là trung điểm của KA,KB
=>ME là đường trung bình của ΔKAB
=>\(ME=\dfrac{AB}{2}\)
mà AB=CD(ABCD là hình chữ nhật)
và \(NC=\dfrac{CD}{2}\)(N là trung điểm của CD)
nên ME=NC
Ta có: ME//AB
CD//AB
Do đó: ME//CD
Xét tứ giác MNCE có
ME//CN
ME=CN
Do đó: MNCE là hình bình hành
d: ta có: MNCE là hình bình hành
=>MN//CE
mà CE\(\perp\)MB
nên MN\(\perp\)MB
nếu BM\(\perp\)CD thì M trùng D mất rồi bạn ạ