Giá trị nhỏ nhất của y=(x-3)^2+1 là
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
31 tháng 7 2017
Đáp án C
Lời giải trên là sai. Cách làm lời giải này chỉ đúng đối với bài toán tìm giá trị lớn nhất – giá trị nhỏ nhất của hàm số trên một đoạn .
Để giải bài toán này, ta lập bảng biến thiên của hàm số y = 2 x 4 − 4 x 2 + 3 trên R
* Bước 1: Tập xác định D = ℝ . Đạo hàm y ' = 8 x 3 − 8 x .
* Bước 2: Cho y ' = 0 tìm x = 0 ; x = − 1 ; x = 1 .
* Bước 3: Ta có bảng biến thiên sau:
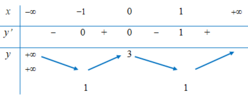
Quan sát bảng biến thiên, ta thấy giá trị nhỏ nhất của hàm số là 1 và hàm số không có giá trị lớn nhất. Vậy lời giải trên sai từ bước 3.
CM
28 tháng 1 2019
Đáp án C
Lưu ý: Đề không cho tìm max – min trên đoạn nên ta không thể so sánh các giá trị như vậy
Cách giải: Lập BBT và ở đây kết luận được giá trị nhỏ nhất của hàm số là 1 , nhưng hàm số không có giá trị lớn nhất.
2 tháng 3 2016
Vì |(x-1)^4-1|\(\ge\)0 với mọi x
(-y^2+3)^2\(\ge\)0 với mọi y
=>...+...\(\ge0\)
Dấu ''='' xảy ra <=>\(\int^{\left(x-1\right)^4-1=0}_{-y^2+3=0}<=>\int^{\left(x-1\right)^4=1}_{y^2=3}\)
Đến đây thì bạn tự giải tiếp nha.OK
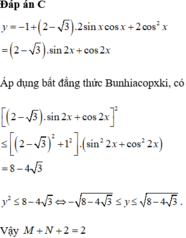
Vì \(\left(x-3\right)^2\ge0\Rightarrow\left(x-3\right)^2+1\ge1\)
\(Ymin=1\) khi \(x-3=0\Leftrightarrow x=3\)