Cho đường tròn \(\left(O;R\right)\) cố định có đường kính AB cố định và CD là đường kính thay đổi không trùng với AB. Tiếp tuyến của đường tròn (O;R) tại B cắt AC và AD lần lượt tại E,F.
a) CMR: CA.CE+DA.DF=\(4R^2\)
b) CM tứ giác CEFD nội tiếp trong một đường tròn
c)Gọi I là tâm của đường tròn ngoại tiếp tứ giác CEFD. Cm điểm I nằm trên một đường tròn cố...
Đọc tiếp
Cho đường tròn \(\left(O;R\right)\) cố định có đường kính AB cố định và CD là đường kính thay đổi không trùng với AB. Tiếp tuyến của đường tròn (O;R) tại B cắt AC và AD lần lượt tại E,F.
a) CMR: CA.CE+DA.DF=\(4R^2\)
b) CM tứ giác CEFD nội tiếp trong một đường tròn
c)Gọi I là tâm của đường tròn ngoại tiếp tứ giác CEFD. Cm điểm I nằm trên một đường tròn cố định.
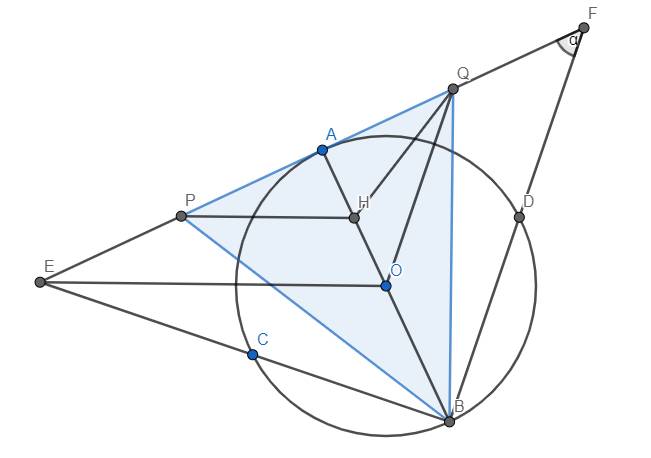
b. Trong tg vuông ABE vuông tại B có BC đường cao nên ^CEB = ^CBA, trong(O) có CBA = ^CDA (chắn cung AC) nên ^CEB = ^CDA suy ra tứ giác CEFD nội tiếp.
c. Gọi P là trung điểm FE, nên AP trung tuyến của tgFAE. Có ^DAP = ^DFP = ^ACD mà ^ADC + ^ACD = 90 nên ^ADC + ADP = 90 nên AP vuông góc CD. Vì I là tâm của đường tròn ngoại tiếp DCEF nên IO vuông góc CD suy ra IO // AP (cùng vuông góc DC) và P trung điểm FE nên IP vuông góc FE vậy IP // AO (cùng vuông góc FE)
Suy ra AOIP là hình bình hành nên IP = AO = R không đổi.
Vậy I chuyển động trên đường thẳng // FE và cách FE khoảng R