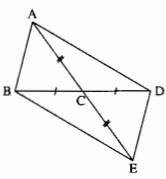
Tìm các tam giác bằng nhau trên hình bên.Giải ra nha các bạn!!
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
1 tháng 2 2019
Giải
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
1 tháng 2 2019
A B C D E
Ta có: ∆ACB = ∆ ECD(c.g.c)
∆ACD = ∆ECB(c.g.c)
∆ABD = ∆EDB(c.g.c)
∆ABE = ∆EDA(c.g.c)
PL
4 tháng 11 2016
Xét tam giác ACI và tam giác BCI , có
CI là cạnh chung
AC = BC
AI= BI
=> tam giác ACI = tam giác BCI
Xét tam giác ACD và tam giác BCD , có
CD là cạnh chung
AD = BD
AC =BC
=> tam giác ACD = tam giác BCD
Xét tam giác ADI và tam giác BDI , có
DI là cạnh chung
AD = BD
AI = BI
=> tam giác ADI = tam giác BDI
ok 3 cặp nha thư
3 tháng 12 2021
Có hai trường hợp:
+ ΔAIC = ΔBIC (c.g.c) vì:
AI = IB (gt)
∠AIC = ∠BIC = 90o
CI chung.
+ ΔAID = ΔBID(c.g.c) vì:
AI = ID (gt)
∠AID = ∠BID = 90o
DI chung.
+ ΔACD = ΔBCD(c.c.c) vì:
AC = BC (Lấy từ ΔAIC = ΔBIC)
AD = BD (Lấy từ ΔAID = ΔBID)
CD chung
22 tháng 10 2016
các góc băng nhau:
ONTˆONT^ == NPKˆNPK^ (đồng vị)
NTOˆNTO^ == PITˆPIT^ (đồng vị)
IPOˆIPO^ == PORˆPOR^ (sole trong)
RONˆRON^ == ONTˆONT^ (sole trong)
-các góc bù nhau:
NTIˆNTI^ và NTOˆNTO^
-các góc ngòai của tam giác TNO:
TNPˆTNP^ ; ITNˆITN^
-tổng các góc trong của tứ giác PROI: 360o
-tổng các góc trong của tứ giác PNTI: 360o
PT
1
CM
17 tháng 5 2018
+ Hai tam giác vuông AMD và AME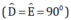 
có:
AM chung
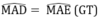
⇒ ΔAMD = ΔAME ( cạnh huyền - góc nhọn)
⇒ MD = ME và AD = AE ( Hai cạnh tương ứng) (1)
+ Hai tam giác vuông MDB và MEC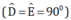 
có
MB = MC (GT)
MD = ME (chứng minh trên)
⇒ ΔMDB = ΔMEC ( cạnh huyền – cạnh góc vuông)
⇒ BD=CE ( hai cạnh tương ứng) (2)
Từ (1) và (2) ⇒ AD+BD=AE+CE ⇒ AB=AC.
+ Xét ΔAMB và ΔAMC có:
MB = MC (GT)
AB = AC (chứng minh trên)
AM chung
⇒ ΔAMB = ΔAMC (c.c.c)
sao mk ko thấy hình nào hết v ?
hình đâu ??????????????????????