giải phương trình sau x+a/x+3 + x-3/x-a =2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 2 2022
\(a,\left(x-6\right)\left(2x-5\right)\left(3x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x-6=0\Leftrightarrow x=6\\2x-5=0\Leftrightarrow x=\dfrac{5}{2}\\3x+9=0\Leftrightarrow x=-3\end{matrix}\right.\)
\(b,2x\left(x-3\right)+5\left(x-3\right)=0\Leftrightarrow\left(2x+5\right)\left(x-3\right)=0\Leftrightarrow\left[{}\begin{matrix}x-3=0\Leftrightarrow x=3\\2x+5=0\Leftrightarrow x=-\dfrac{5}{2}\end{matrix}\right.\)
\(c,x^2-4-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\Leftrightarrow\left[{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
\(x=-7\left(2m-5\right)x-2m^2+8\Leftrightarrow x+7\left(2m-5\right)=8-2m^2\Leftrightarrow x\left(14m-34\right)=8-2m^2\)
\(ycđb\Leftrightarrow14m-34\ne0\Leftrightarrow m\ne\dfrac{34}{14}\)\(\Rightarrow x=\dfrac{8-2m^2}{14m-34}\)
\(3.17\Leftrightarrow4x^2-4x+1-2x-1=0\Leftrightarrow4x^2-6x=0\Leftrightarrow x\left(4x-6\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=\dfrac{3}{2}\end{matrix}\right.\)
DT
16 tháng 2 2022
3.15:
a, \(\Leftrightarrow\left\{{}\begin{matrix}x-6=0\\2x-5=0\\3x+9=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=6\\x=\dfrac{5}{2}\\x=-\dfrac{9}{3}=-3\end{matrix}\right.\)
b, \(\Leftrightarrow\left(x-3\right)\left(2x+5\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-3=0\\2x+5=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=3\\x=-\dfrac{5}{2}\end{matrix}\right.\)
c, \(\Leftrightarrow\left(x-2\right)\left(x+2\right)-\left(x-2\right)\left(3-2x\right)=0\)
\(\Leftrightarrow\left(x-2\right)\left(x+2-3+2x\right)=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2=0\\3x-1=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=2\\x=\dfrac{1}{3}\end{matrix}\right.\)
3.16
\(\Leftrightarrow\left(2m-5\right).-7-2m^2+8=0\)
\(\Leftrightarrow-14m+35-2m^2+8=0\)
\(\Leftrightarrow-14m-2m^2+43=0\)
\(\Leftrightarrow-2\left(7m+m^2\right)=-43\)
\(\Leftrightarrow m\left(7-m\right)=\dfrac{43}{2}\)
\(\Leftrightarrow\dfrac{m\left(7-m\right)}{1}-\dfrac{43}{2}=0\)
\(\Leftrightarrow\dfrac{14m-2m^2}{2}-\dfrac{43}{2}=0\)
pt vô nghiệm
5 tháng 2 2022
Bài 3:
b: \(\Leftrightarrow x^2\left(x+1\right)^2=0\)
hay \(x\in\left\{0;-1\right\}\)
c: \(\Leftrightarrow\left(x-1\right)\left(x^2+x+1\right)=0\)
=>x-1=0
hay x=1
d: \(\Leftrightarrow6x^2-3x-4x+2=0\)
\(\Leftrightarrow\left(2x-1\right)\left(3x-2\right)=0\)
hay \(x\in\left\{\dfrac{1}{2};\dfrac{2}{3}\right\}\)
Y
12 tháng 4 2022
\(a,\dfrac{x-3}{x}=\dfrac{x-3}{x+3}\)\(\left(đk:x\ne0,-3\right)\)
\(\Leftrightarrow\dfrac{x-3}{x}-\dfrac{x-3}{x+3}=0\)
\(\Leftrightarrow\dfrac{\left(x-3\right)\left(x+3\right)-x\left(x-3\right)}{x\left(x+3\right)}=0\)
\(\Leftrightarrow x^2-9-x^2+3x=0\)
\(\Leftrightarrow3x-9=0\)
\(\Leftrightarrow3x=9\)
\(\Leftrightarrow x=3\left(n\right)\)
Vậy \(S=\left\{3\right\}\)
Y
12 tháng 4 2022
\(b,\dfrac{4x-3}{4}>\dfrac{3x-5}{3}-\dfrac{2x-7}{12}\)
\(\Leftrightarrow\dfrac{4x-3}{4}-\dfrac{3x-5}{3}+\dfrac{2x-7}{12}>0\)
\(\Leftrightarrow\dfrac{3\left(4x-3\right)-4\left(3x-5\right)+2x-7}{12}>0\)
\(\Leftrightarrow12x-9-12x+20+2x-7>0\)
\(\Leftrightarrow2x+4>0\)
\(\Leftrightarrow2x>-4\)
\(\Leftrightarrow x>-2\)
H
11 tháng 5 2023
`|5x| = - 3x + 2`
Nếu `5x>=0<=> x>=0` thì phương trình trên trở thành :
`5x =-3x+2`
`<=> 5x +3x=2`
`<=> 8x=2`
`<=> x= 2/8=1/4` ( thỏa mãn )
Nếu `5x<0<=>x<0` thì phương trình trên trở thành :
`-5x = -3x+2`
`<=>-5x+3x=2`
`<=> 2x=2`
`<=>x=1` ( không thỏa mãn )
Vậy pt đã cho có nghiệm `x=1/4`
__
`6x-2<5x+3`
`<=> 6x-5x<3+2`
`<=>x<5`
Vậy bpt đã cho có tập nghiệm `x<5`
S
23 tháng 2 2021
Mình khuyên bạn thế này :
Bạn nên tách những câu hỏi ra
Như vậy các bạn sẽ dễ giúp
Và cũng có nhiều bạn giúp hơn !
23 tháng 2 2021
Bài 1.
a) ( x - 3 )( x + 7 ) = 0
<=> x - 3 = 0 hoặc x + 7 = 0
<=> x = 3 hoặc x = -7
Vậy S = { 3 ; -7 }
b) ( x - 2 )2 + ( x - 2 )( x - 3 ) = 0
<=> ( x - 2 )( x - 2 + x - 3 ) = 0
<=> ( x - 2 )( 2x - 5 ) = 0
<=> x - 2 = 0 hoặc 2x - 5 = 0
<=> x = 2 hoặc x = 5/2
Vậy S = { 2 ; 5/2 }
c) x2 - 5x + 6 = 0
<=> x2 - 2x - 3x + 6 = 0
<=> x( x - 2 ) - 3( x - 2 ) = 0
<=> ( x - 2 )( x - 3 ) = 0
<=> x - 2 = 0 hoặc x - 3 = 0
<=> x = 2 hoặc x = 3
CM
21 tháng 1 2019
a) |3x| = x + 6 (1)
Ta có 3x = 3x khi x ≥ 0 và 3x = -3x khi x < 0
Vậy để giải phương trình (1) ta quy về giải hai phương trình sau:
+ ) Phương trình 3x = x + 6 với điều kiện x ≥ 0
Ta có: 3x = x + 6 ⇔ 2x = 6 ⇔ x = 3 (TMĐK)
Do đó x = 3 là nghiệm của phương trình (1).
+ ) Phương trình -3x = x + 6 với điều kiện x < 0
Ta có -3x = x + 6 ⇔ -4x + 6 ⇔ x = -3/2 (TMĐK)
Do đó x = -3/2 là nghiệm của phương trình (1).
Vậy tập nghiệm của phương trình đã cho S = {3; -3/2}
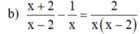
ĐKXĐ: x ≠ 0, x ≠ 2
Quy đồng mẫu hai vễ của phương trình, ta được:
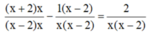
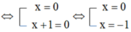
Vậy tập nghiệm của phương trình là S = {-1}
c) (x + 1)(2x – 2) – 3 > –5x – (2x + 1)(3 – x)
⇔ 2x2 – 2x + 2x – 2 – 3 > –5x – (6x – 2x2 + 3 – x)
⇔ 2x2 – 5 ≥ –5x – 6x + 2x2 – 3 + x
⇔ 10x ≥ 2 ⇔ x ≥ 1/5
Tập nghiệm: S = {x | x ≥ 1/5}
12 tháng 5 2023
1:
a: =>3x=6
=>x=2
b: =>4x=16
=>x=4
c: =>4x-6=9-x
=>5x=15
=>x=3
d: =>7x-12=x+6
=>6x=18
=>x=3
2:
a: =>2x<=-8
=>x<=-4
b: =>x+5<0
=>x<-5
c: =>2x>8
=>x>4
LA
24 tháng 3 2017
a/ 4x + 20 = 0
⇔4x = -20
⇔x = -5
Vậy phương trình có tập nghiệm S = {-5}
b/ 2x – 3 = 3(x – 1) + x + 2
⇔ 2x-3 = 3x -3+x+2
⇔2x – 3x = -3+2+3
⇔-2x = 2
⇔x = -1
Vậy phương trình có tập nghiệm S = {-1}
LA
24 tháng 3 2017
câu tiếp theo
a/ (3x – 2)(4x + 5) = 0
3x – 2 = 0 hoặc 4x + 5 = 0
- 3x – 2 = 0 => x = 3/2
- 4x + 5 = 0 => x = – 5/4
Vậy phương trình có tập nghiệm S= {-5/4,3/2}
b/ 2x(x – 3) – 5(x – 3) = 0
=> (x – 3)(2x -5) = 0
=> x – 3 = 0 hoặc 2x – 5 = 0
* x – 3 = 0 => x = 3
* 2x – 5 = 0 => x = 5/2
Vậy phương trình có tập nghiệm S = {0, 5/2}
ĐKXĐ : x \(\ne\)-3 ; x \(\ne\)a
\(\frac{x+a}{x+3}+\frac{x-3}{x-a}=2\)( 1 )
\(\frac{x^2-a^2+x^2-9}{\left(x+3\right)\left(x-a\right)}=2\)
\(\frac{2x^2-a^2-9}{x^2+3x-ax-3a}=2\)
\(2x^2-a^2-9=2x^2+6x-2ax-6a\)( 2 )
\(2ax-6x=a^2-6a+9\)
\(2x\left(a-3\right)=\left(a-3\right)^2\)
+) nếu a = 3 thì phương trình ( 2 ) có dạng 0x = 0 ( vô số nghiệm )
Để nghiệm tùy ý này là nghiệm của ( 1 ) thì x \(\ne\)\(\pm3\)
+) nếu a \(\ne\)3 thì phương trình ( 2 ) có nghiệm x = \(\frac{\left(a-3\right)^2}{2\left(a-3\right)}=\frac{a-3}{2}\)
Để nghiệm này là nghiệm của ( 1 ) thì ta có :
\(\frac{a-3}{2}\ne-3\)và \(\frac{a-3}{2}\ne a\), tức là a \(\ne\)-3
Vậy nếu a \(\ne\)\(\pm3\)thì x = \(\frac{a-3}{2}\)là nghiệm của ( 1 )
Kết luận : nếu a = 3 thì phương trình đã cho có nghiệm tùy ý x \(\ne\)\(\pm3\)
nếu a \(\ne\)\(\pm3\)thì phương trình đã cho có 1 nghiệm x = \(\frac{a-3}{2}\)
nếu a = -3 thì phương trình đã cho vô nghiệm
đây mình làm cực kỳ hoàn hảo, trình bày ok luôn nhé