Cho tam giac ABC vuông tại A , M là trung điểm của BC , chứng minh rằng AM=1/2 BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
EH
27 tháng 10 2018
A B C M N
∆ABC có M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm N sao cho MN = MA.
Ta có:
ےAMB = ےNMC (đối đỉnh)
BM = CM (giả thiết)
MA = MN (dựng hình)
Suy ra: ∆MAB = ∆MNC (c.g.c)
Suy ra: NC = AB và ےMBA = ےMCN
Do ےMBA = ےMCN nên AB // NC
Suy ra ےBAC + ےACN = 180
Ta có: ےBAC = 90 nên ےACN = 90
=> ∆ABC = ∆CNA (c.g.c) vì AC là cạnh chung
AB = NC (cmt) và ےBAC = ےACN = 90
=> AN = BC
=> AM = \(\frac{1}{2}BC\)
=>CMT
19 tháng 1 2017
vẽ thêm MD song song AH
MH song song AD
Xét tam giác MDA và tam giác AHM có
Góc A1 = góc M2 (so le trong)
Góc A2 = góc M1 ( so le trong)
AM là cạnh chung
\(\Rightarrow\)Tam giác MDA = tam giác AHM (g.c.g)
\(\Rightarrow\)MD = AH (2 cạnh tương ứng)
Xét tam giác MBD và tam giác CMH có
Góc BMD = góc MCH (đồng vị)
Góc D1 = góc H2 (=90)
BM = MC (giả thiết)
\(\Rightarrow\)Tam giác MBD = tam giác CMH (cạnh huyền - góc nhọn)
\(\Rightarrow\)BD = MH ( 2 cạnh tương ứng)
Xét tam giác BDM và tam giác MHA có
MD = AH ( cmt)
Góc D2 = góc H1 (=90)
BD = MH (cmt)
\(\Rightarrow\)tam giác MBD = tam giác MAH ( c.g.c)
\(\Rightarrow\)BM = AM (2 cạnh tương ứng)
Vì BM = MC và AM = BM
\(\Rightarrow\)AM = MC
Mà BC = BM + MC
\(\Rightarrow\)BC = 2*AM
\(\Rightarrow\)AM = \(\frac{1}{2}\cdot BC\)
Vậy AM = \(\frac{1}{2}\cdot BC\)
KV
25 tháng 5 2023
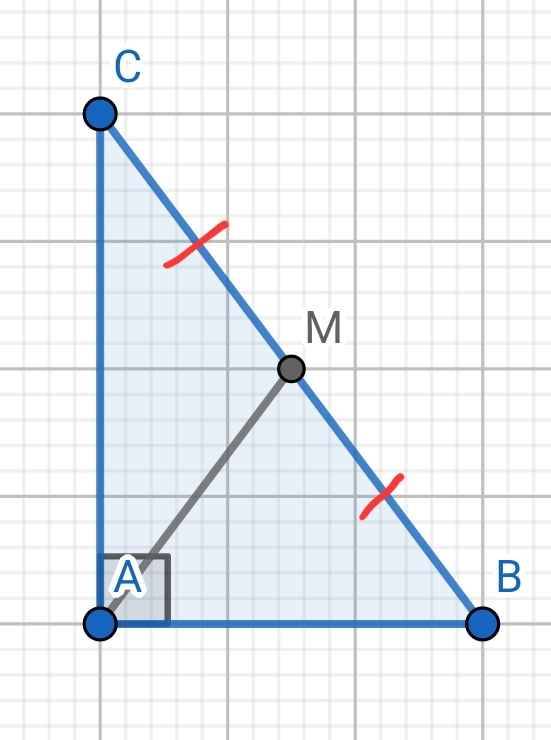
a) ∆ABC vuông tại A
M là trung điểm BC
⇒ AM là đường trung tuyến ứng với cạnh huyền BC
⇒ AM = BM = CM = BC : 2
b) ∆ABC vuông tại A có ∠C = 30⁰
⇒ ∠B = 90⁰ - 30⁰ = 60⁰
Do AM = BM (cmt)
⇒ ∆ABM cân tại M
Lại có ∠ABM = ∠B = 60⁰
⇒ ∆ABM đều
⇒ AB = AM = BM = BC : 2
2 tháng 1 2019
a) Chứng minh tam giac AMB = tam giac DMC
Xét tam giác MAB và tam giác MDC, có
- MA = MD (M là trung điểm AD)
- MB = MD (M là trung điểm BD)
- Góc M đối nhau
=> tam giác MAB = tam giác MDC (cạnh - góc - cạnh) (đpcm)
b) Chứng minh DC vuông góc AC
Ta có góc BAC = 90 độ (tam giác ABC vuông tại A)
=> góc A1 + góc A2 = 90 độ
mà góc A1 = góc CDA (do tam giác MAB = tam giác MDC chứng minh trên)
=> góc ADC + góc A2 = 90 độ
Xét tam giác CAD,
có: góc ACD = 180 độ - (góc ADC + góc A2) = 180 độ - 90 độ = 90 độ
=> góc ACD = 90 độ
=> tam giác DAC vuông tại C
Ta có DC vuông góc AC tại C
và BA vuông góc AC tại A
=> BA // DC (đpcm)
c) AM = 1/2BC
Câu này áp dụng định lý: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền => AM = 1/2 BC (đpcm)
Còn nếu yêu cầu phải trình bày cách làm, thì bạn làm như phía dưới:
Xét tứ giác ABDC có:
- BA = CD (do tam giác MAB = tam gia MDC (chứng minh trên)
- DC // BA
=> tứ giác ABDC là hình bình hành
và có góc A vuông
=> tứ giác ABDC là hình chữ nhật
=> 2 đường chéo của hình chữ nhật là AD = BC
mà M là trung điểm của AD và BC
=> AM = 1/2 BC (đpcm)
26 tháng 8 2021
Trên tia đối của tia MA, lấy điểm D sao cho MA=MD
Xét tứ giác ACDB có
M là trung điểm của đường chéo BC
M là trung điểm của đường chéo AD
Do đó: ACDB là hình bình hành
Hình bình hành ACDB có \(\widehat{CAB}=90^0\)
nên ACDB là hình chữ nhật
Suy ra: BC=AD
mà \(AM=\dfrac{1}{2}AD\)
nên \(AM=\dfrac{1}{2}BC\)
Xét tam giác ABC vuông tại A
Có M là trung điểm của BC
=> AM là trung tuyến của BC.
=> AM=BM=MC=1/2 BC ( Định lý)