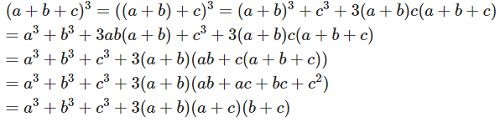Cho \(a^3+b^3+c^3=-1\) và \(a+b+c=-1\)
Tính tổng \(a^{2019}+b^{2019}+c^{2019}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 4 2020
\(a+b+c = 1 ; 1/a + 1/b + 1/c = 1 \)
\(=> (a+b+c)(1/a +1/b+1/c) = 1\)
\(<=> a/b + b/a + a/c + c/a + b/c + c/b + 3 - 1 = 0\)
\(<=> (a^2+b^2)/ab + (a^2+c^2)/ac + (b^2+c^2)/bc + 2 =0\)
\(<=> (a^2 + b^2).c + (a^2+c^2).b + (b^2+c^2).a + 2abc = 0\)
\(<=> a^2c + b^2c + a^2b + c^2b + ab^2 + ac^2 + 2abc =0 \)
\(<=> a^2c + ac^2 + abc + a^2b+ ab^2 + abc + b^2c + bc^2 =0\)
\(<=> ac(a+b+c) + ab(a+b+c) + bc(b+c) =0 \)
\(<=> a(b+c)(a+b+c) + bc(b+c) =0 \)
\(<=> (b+c)(a^2 + ab + ac + bc ) = 0 \)
\(<=> (b+c)[a(a+b) + c(a+b)] =0\)
\(<=> (b+c)(a+b)(a+c) =0 \)
<=> 1 trong 3 số \(b+c;a+b ; a+c = 0\)
\(a+b=0 => a= -b => a + b + c = 1 <=> c = 1 ; a = b = 0\)
Thay vào S ta được : \(\Rightarrow S=0^{2019}+0^{2019}+1^{2019}=1\)
Ta có: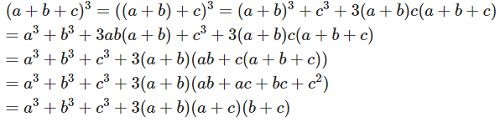
\(\Rightarrow3\left(a+b\right)\left(b+c\right)\left(c+a\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}a+b=0\\b+c=0\\c+a=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=-b,c=-1\\b=-c,a=-1\\c=-a,b=-1\end{matrix}\right.\)
Trường hợp a = -b
\(\Rightarrow a^{2019}+b^{2019}+c^{2019}=\left(-b\right)^{2019}+b^{2019}+c^{2019}=c^{2019}=\left(-1\right)^{2019}=-1\)
Các trường hợp khác tương tự đều có kq = -1
Ta Co: