Cho biểu thức: A= 2t2(m - 1) - t(m - 1)(2t - 1) + t +m với m là tham số. Rút gọn A.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HN
2
NH
18 tháng 2 2020
a) \(A=2t^2\left(m-1\right)-t\left(m-1\right)\left(2t-1\right)+t+m\)
\(A=2t^2m-2t^2-2t^2m+tm+2t^2-t+t+m\)
\(A=tm+m\)
b) Ta có:
\(t.2+2=0\)
\(\Leftrightarrow2t+2=0\)
\(\Leftrightarrow2t=-2\)
\(\Leftrightarrow t=-1\)
vậy: phương trình có tập nghiệm là: S = {-1}
t không chắc :v
3 tháng 4 2020
a) A = [2t2(m - 1) - t(m - 1)(2t - 1)] + t + m
A = t(m - 1)[2t - (2t - 1)] + t + m
A = t(m - 1) + t + m
A = tm + m
b) Với m = 2; A = 0 thì ta được pt:
0 = 2t + 2
⇔ t = -1
Vậy khi m = 2 và để A = 0 thì t = -1
28 tháng 1 2022
1, Với x >= 0 ; x khác 1
\(P=\dfrac{\sqrt{x}\left(x-1\right)+2\sqrt{x}\left(\sqrt{x}-1\right)-\left(3x+1\right)\left(\sqrt{x}+1\right)}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x\sqrt{x}+2x-3\sqrt{x}-3x\sqrt{x}-3x-\sqrt{x}-1}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{-2x\sqrt{x}-x-4\sqrt{x}-1}{\left(x-1\right)\left(\sqrt{x}+1\right)}\)
28 tháng 1 2022
mình sửa đề câu 2 nhé
a, \(x^2+mx-1=0\)
\(\Delta=m^2-4\left(-1\right)=m^2+4>0\)
Vậy pt luôn có 2 nghiệm pb
b, Theo Vi et : \(\left\{{}\begin{matrix}x_1+x_2=-m\\x_1x_2=-1\end{matrix}\right.\)
Ta có : \(\left(x_1+x_2\right)^2-2x_1x_2=7\)
Thay vào ta được : \(m^2+2=7\Leftrightarrow m^2=5\Leftrightarrow m=\pm\sqrt{5}\)
25 tháng 1 2023
a: \(P=\left(\dfrac{1}{m\left(m-1\right)}+\dfrac{1}{m-1}\right)\cdot\dfrac{\left(m-1\right)^2}{m+1}\)
\(=\dfrac{m+1}{m\left(m-1\right)}\cdot\dfrac{\left(m-1\right)^2}{m+1}=\dfrac{m-1}{m}\)
b: Khi m=1/2 thì \(P=\left(\dfrac{1}{2}-1\right):\dfrac{1}{2}=\dfrac{-1}{2}\cdot2=-1\)
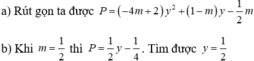
\(=2t^2m-2t^2-t\left(2tm-m-2t+1\right)+t+m\)
\(=2t^2m-2t^2-2t^2m+tm+2t^2-t+t+m\)
=tm+m