Cho tam giác ABC có \(\widehat{A}=90^o\). Đường phân giác BD=\(6\sqrt{5}\)cm và 5AD=3DC. Tính BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
4 tháng 12 2023
a: ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(BC^2=6^2+8^2=36+64=100\)
=>\(BC=\sqrt{100}=10\left(cm\right)\)
Xét ΔABC có BD là phân giác
nên \(\dfrac{DA}{AB}=\dfrac{DC}{BC}\)
=>\(\dfrac{DA}{6}=\dfrac{DC}{10}\)
=>\(\dfrac{DA}{3}=\dfrac{DC}{5}\)
mà DA+DC=AC=8cm(D nằm giữa A và C)
nên \(\dfrac{DA}{3}=\dfrac{DC}{5}=\dfrac{DA+DC}{3+5}=\dfrac{8}{8}=1\)
=>\(DA=3\cdot1=3cm;DC=5\cdot1=5cm\)
b: ΔABC vuông tại A
mà AM là đường trung tuyến
nên \(AM=MB=MC=\dfrac{BC}{2}=5\left(cm\right)\)
mà DC=5cm
nên CM=CD
Xét ΔCDI và ΔCMI có
CD=CM
\(\widehat{DCI}=\widehat{MCI}\)
CI chung
Do đó: ΔCDI=ΔCMI
=>\(\widehat{CID}=\widehat{CIM}\) và \(\widehat{IMC}=\widehat{IDC}\)(3)
Ta có: \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}\)(góc IDC là góc ngoài tại đỉnh D của ΔABD)
nên \(\widehat{IDC}=\widehat{BAD}+\widehat{ABD}=90^0+\widehat{ABD}\)(2)
Xét ΔBIM có \(\widehat{IMC}\) là góc ngoài tại đỉnh M
nên \(\widehat{IMC}=\widehat{MIB}+\widehat{MBI}\left(1\right)\)
Từ (1),(2),(3) suy ra \(\widehat{MIB}+\widehat{MBI}=90^0+\widehat{ABD}\)
mà \(\widehat{MBI}=\widehat{ABD}\)
nên \(\widehat{MIB}=90^0\)
25 tháng 2 2020
a. Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
BC2 = AB2 + AC2 = 122 + 162 = 400
Suy ra: BC =20 (cm)
Vì AD là đường phân giác của ∠(BAC) nên:
(tỉnh chất đường phân giác)
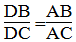
Suy ra: 
Suy ra: 
Vậy : DC = BC – DB = 20 - 60/7 = 80/7 (cm)
b. Ta có: SABC =1/2.AB.AC =1/2.AH.BC
Suy ra: AB.AC = AH.BC
Trong tam giác vuông AHB, ta có: ∠(AHB ) = 90o
Theo định lí Pi-ta-go, ta có: AB2 = AH2 + HB2
Suy ra: HB2 = AB2 - AH2 = 122 - (9,6)2 = 51,84 ⇒ HB =7,2 (cm)
Vậy HD = BD – HB = 607 - 7,2 ≈ 1,37 (cm)
Trong tam giác vuông AHD, ta có: ∠(AHD) = 90o
Theo định lí Pi-ta-go, ta có:
AD2 = AH2 + HD2 = (9,6)2 + (1,37)2 = 94,0369
Suy ra: AD ≈ 9,70 (cm)
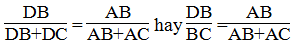
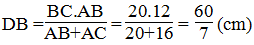
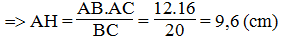
A B C D 1 2 6v5
( v là căn nha bạn ; Ví dụ 8v5 là 8căn5 nha )
Ta có : \(SinABC=\frac{AC}{BC}\)
Mà : gócABC = 2.gócB2 ( BD là đường phân giác )
Do đó : \(SinABC=2.SinB_2\)
\(\Rightarrow sinB_2=\frac{1}{2}SinABC=\frac{1}{2}.\frac{AC}{BC}=\frac{AC}{2BC}\)
Ta có : \(SinB_1=\frac{AD}{BD}\)
Mà : góc B1 = góc B2 ( BD là đường phân giác )
\(\Rightarrow\frac{AD}{BD}=\frac{AC}{2BC}\)
\(\Rightarrow2BC=\frac{AC.BD}{AD}\)
\(\Rightarrow BC=\frac{AC.BD}{2.AD}=\frac{\left(AD+DC\right).6v5}{2.AD}\) ( 1 )
Ta có : 5AD = 3DC ( gt )
\(\Rightarrow AD=\frac{3DC}{5}=\frac{3}{5}DC\)
Thay : \(AD=\frac{3}{5}DC\) vào ( 1 ) Ta được :
\(BC=\frac{6v5.\left(\frac{3}{5}DC+DC\right)}{2.\left(\frac{3}{5}DC\right)}\)
\(BC=\frac{6v5.\left(\frac{8}{5}DC\right)}{\frac{6}{5}DC}\)
\(BC=\frac{\frac{48v5}{5}DC}{\frac{6}{5}DC}\)
\(BC=\frac{48v5}{6}\)
\(BC=8v5\)
Vậy BC = 8v5 cm
Học tốt !!!