Nếu \(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{a+b}\) (với a,b\(\ne\)0; a\(\ne\)-b) thì giá trị của biểu thức \(\dfrac{b}{a}+\dfrac{a}{b}\) là:........
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
19 tháng 12 2017
\(\frac{1}{c}=\frac{1}{2}\left(\frac{1}{a}+\frac{1}{b}\right)\)
\(\frac{1}{c}:\frac{1}{2}=\frac{1}{a}+\frac{1}{b}\)
\(\frac{2}{c}=\frac{a+b}{ab}\)
\(\Rightarrow2ab=ac+bc\)
\(\Rightarrow ac-ab=ab-bc\)
\(\Rightarrow a.\left(c-b\right)=b.\left(a-c\right)\)
\(\Rightarrow\frac{a}{b}=\frac{a-c}{c-b}\)( đpcm )
11 tháng 7 2021
Ta có: \(\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\left(\dfrac{c}{abc}+\dfrac{b}{abc}+\dfrac{a}{abc}\right)}\)
\(=\sqrt{\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}-2\cdot\dfrac{a+b+c}{abc}}\)
\(=\sqrt{\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2}=\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\)
17 tháng 5 2018
\(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\) hả Lặng Thầm
8 tháng 9 2017
Ta có: \(\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\)
\(=\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}+\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}\)
Ta cần chứng minh: \(\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}=0\) thật vậy:
\(\dfrac{2}{ab}+\dfrac{2}{bc}+\dfrac{2}{ac}=\dfrac{2\left(a+b+c\right)}{abc}=\dfrac{2.0}{abc}=0\)Tức là:\(\dfrac{1}{a^2}+\dfrac{1}{b^2}+\dfrac{1}{c^2}=\left(\dfrac{1}{a}+\dfrac{1}{b}+\dfrac{1}{c}\right)^2\left(đpcm\right)\)
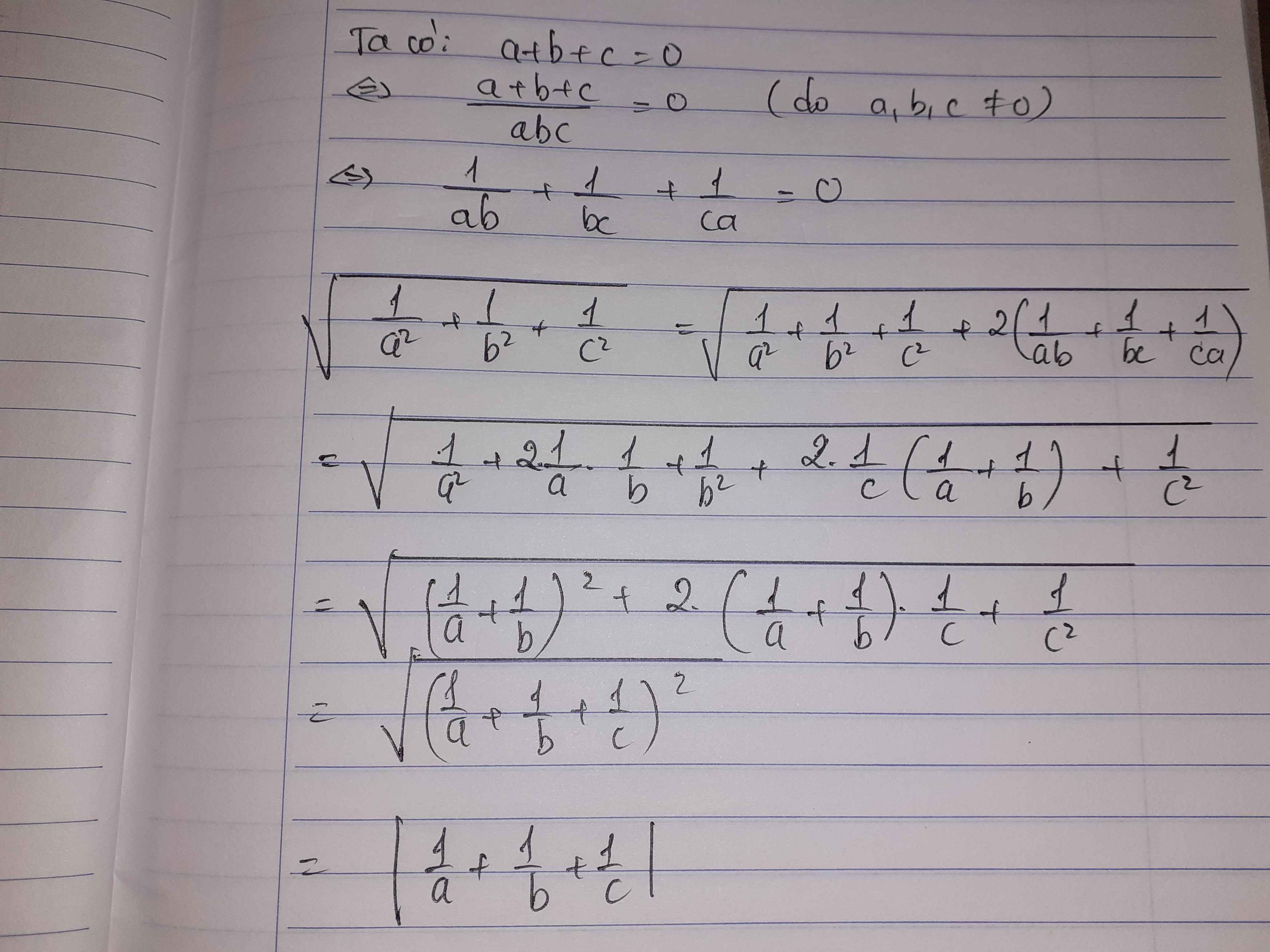
\(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{1}{a+b}\Leftrightarrow\dfrac{a+b}{ab}=\dfrac{1}{a+b}\)
\(\Leftrightarrow\left(a+b\right)^2=ab\)
\(\Rightarrow\dfrac{b}{a}+\dfrac{a}{b}=\dfrac{a^2+b^2}{ab}=\dfrac{\left(a+b\right)^2-2ab}{ab}=\dfrac{ab-2ab}{ab}=\dfrac{-ab}{ab}=-1\)
Ta có:
\(\dfrac{1}{a}+\dfrac{1}{b}=\dfrac{a+b}{ab}\Rightarrow\dfrac{a+b}{ab}=\dfrac{1}{a+b}\)
\(\Leftrightarrow ab=\left(a+b\right)^2\)
Vậy, \(\dfrac{b}{a}+\dfrac{a}{b}=\dfrac{a^2+b^2}{ab}=\dfrac{a^2+2ab+b^2-2ab}{ab}=\dfrac{\left(a+b\right)^2-2ab}{ab}=\dfrac{ab-2ab}{ab}=\dfrac{-ab}{ab}=-1\)