Giusp mình 
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
TQ
1

HL
24 tháng 3 2022
\(M=\frac{3}{2}+\frac{3}{6}+\frac{3}{12}+...+\frac{3}{2021.2022}\)
\(=3\left(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{2021.2022}\right)\)
\(=3\left(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+...+\frac{1}{2021}-\frac{1}{2022}\right)\)
\(=3\left(1-\frac{1}{2022}\right)\)
\(=3.\frac{2021}{2022}\)
\(=\frac{6063}{2022}\)

25 tháng 6 2023
Sau lần 2 còn (5+5):1/2=20(kg)
Sau lần 1 còn (20+4):2/3=24*3/2=36(kg)
Trước khi bán có:
(36+3):3/4=39*4/3=52(kg)

27 tháng 7 2023
a: xN,xO,xO,xM,NO,NM,Nx,My,MO
b: ON và OM
c; NO và Nx
d: Mx và My
e: Còn gọi là tia OM





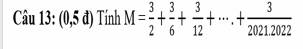 Giusp mình vs ạ,mình cần gấp
Giusp mình vs ạ,mình cần gấp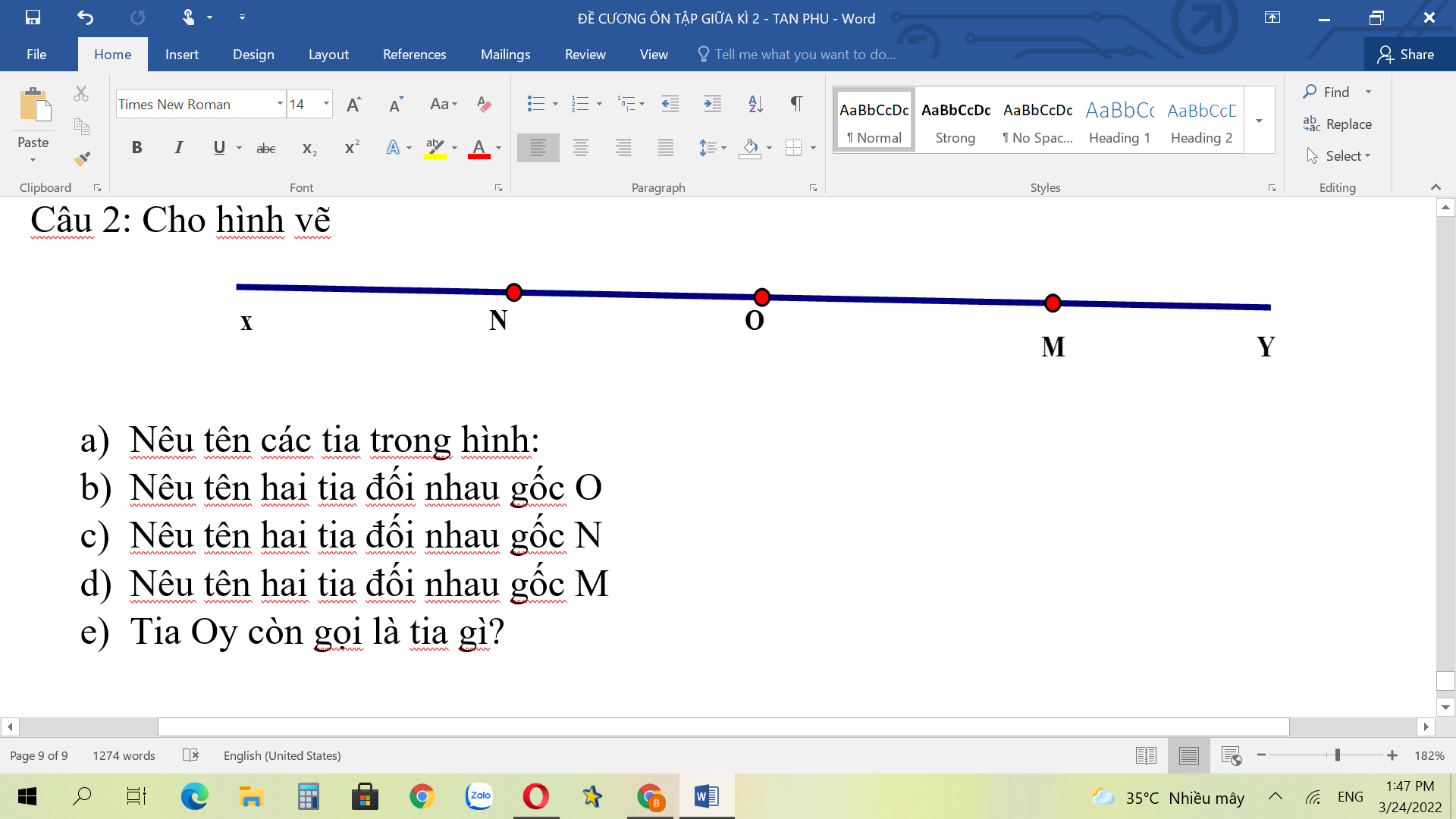





Bài 8:
a) \(x^2-2x+1=25\)
\(\Rightarrow\left(x-1\right)^2=25\)
\(\Rightarrow\orbr{\begin{cases}\left(x-1\right)^2=5^2\\\left(x-1\right)^2=\left(-5\right)^2\end{cases}}\Rightarrow\orbr{\begin{cases}x-1=5\\x-1=-5\end{cases}}\Rightarrow\orbr{\begin{cases}x=6\\x=-4\end{cases}}\)
b) \(\left(5x+1\right)^2-\left(5x-3\right)\left(5x+3\right)=30\)
\(\Rightarrow25x^2+10x+1-25x^2+9=30\)
\(\Rightarrow10x+10=30\)
\(\Rightarrow10x=20\)
\(\Rightarrow x=2\)
c) \(\left(x-1\right)\left(x^2+x+1\right)-x\left(x+2\right)\left(x-2\right)=5\)
\(\Rightarrow x^3-1-x\left(x^2-4\right)=5\)
\(\Rightarrow x^3-1-x^3+4x=5\)
\(\Rightarrow4x=6\)
\(\Rightarrow x=\frac{3}{2}\)
d) \(\left(x-2\right)^3-\left(x-3\right)\left(x^2+3x+9\right)+6\left(x+1\right)^2=15\)
\(\Rightarrow x^3-6x^2+12x-8-\left(x^3-27\right)+6\left(x^2+2x+1\right)=15\)
\(\Rightarrow x^3-6x^2+12x-8-x^3+27+6x^2+12x+6=15\)
\(\Rightarrow24x+25=15\)
\(\Rightarrow24x=-10\)
\(\Rightarrow x=\frac{-5}{12}\)
Bài 9:
a) \(-x^2+6x-15=-x^2+6x-9-6=-\left(x^2-6x+9\right)-6=-\left(x-3\right)^2-6\)
Ta có: \(\left(x-3\right)^2\ge0\Rightarrow-\left(x-3\right)^2\le0\Rightarrow-\left(x-3\right)^2-6\le-6\)
\(\Rightarrow-x^2+6x-15\) luôn âm với mọi \(x\)
b) \(-9x^2+24x-18=-9x^2+24x-16-2=-\left(9x^2-24x+16\right)-2=-\left(3x-4\right)^2-2\)
Ta có: \(\left(3x-4\right)^2\ge0\Rightarrow-\left(3x-4\right)^2\le0\Rightarrow-\left(3x-4\right)^2-2\le2\)
\(\Rightarrow-9x^2+24x-18\) luôn âm với mọi \(x\)
c) \(\left(x-3\right)\left(1-x\right)-2=x\left(1-x\right)-3\left(1-x\right)-2=x-x^2-3+3x-2=-x^2+4x-5\)
\(=-x^2+4x-4-1=-\left(x^2-4x+1\right)-1=-\left(x-1\right)^2-1\)
Ta có: \(\left(x-1\right)^2\ge0\Rightarrow-\left(x-1\right)^2\le0\Rightarrow-\left(x-1\right)^2-1\le-1\)
\(\Rightarrow\left(x-3\right)\left(1-x\right)-2\) luôn âm với mọi x
d) \(\left(x+4\right)\left(2-x\right)-10=x\left(2-x\right)+4\left(2-x\right)-10=2x-x^2+8-4x-10=-x^2-2x-2\)
\(=-x^2-2x-1-1=-\left(x^2+2x+1\right)-1=-\left(x+1\right)^2-1\)
Ta có: \(\left(x+1\right)^2\ge0\Rightarrow-\left(x+1\right)^2\le0\Rightarrow-\left(x+1\right)^2-1\le-1\)
\(\Rightarrow\left(x+4\right)\left(2-x\right)-10\) luôn âm với mọi \(x\)