X2 -- 9x =0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(a.x^2-7x-3x+21=0\Leftrightarrow\left(x^2-7x\right)-\left(3x-21\right)=0\)
\(\Leftrightarrow x\left(x-7\right)-3\left(x-7\right)=0\Leftrightarrow\left(x-3\right)\left(x-7\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=7\end{matrix}\right.\)
\(b.x^2+6x+2x+12=0\Leftrightarrow\left(x^2+6x\right)+\left(2x+12\right)=0\)
\(\Leftrightarrow x\left(x+6\right)+2\left(x+6\right)=0\Leftrightarrow\left(x+2\right)\left(x+6\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-2\\x=-6\end{matrix}\right.\)
\(c.x^2+4x+5x+20=0\Leftrightarrow\left(x^2+4x\right)+\left(5x+20\right)=0\)
\(\Leftrightarrow x\left(x+4\right)+5\left(x+4\right)=0\Leftrightarrow\left(x+5\right)\left(x+4\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-5\\x=-4\end{matrix}\right.\)

\(a,5x\left(x^2-9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x^2=9\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ b,3\left(x+3\right)-x^2-3x=0\\ \Leftrightarrow3\left(x+3\right)-x\left(x+3\right)=0\\ \Leftrightarrow\left(x+3\right)\left(3-x\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=3\\x=-3\end{matrix}\right.\\ c,x^2-9x-10=0\\ \Leftrightarrow x^2+x-10x-10=0\\ \Leftrightarrow x\left(x+1\right)-10\left(x+1\right)=0\\ \Leftrightarrow\left(x-10\right)\left(x+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
a, 5\(x\)(\(x^2\) - 9) = 0
\(\left[{}\begin{matrix}x=0\\x^2-9=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\)
Vậy \(x\) \(\in\) { -3; 0; 3}
b, 3.(\(x+3\)) - \(x^2\) - 3\(x\) = 0
3.(\(x+3\)) - \(x\).( \(x\) + 3) = 0
(\(x+3\))( 3 - \(x\)) = 0
\(\left[{}\begin{matrix}x=-3\\x=3\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -3; 3}
c, \(x^2\) - 9\(x\) - 10 = 0
\(x^2\) + \(x\) - 10\(x\) - 10 = 0
\(x.\left(x+1\right)\) - 10.( \(x-1\)) = 0
(\(x+1\))(\(x-10\)) = 0
\(\left[{}\begin{matrix}x+1=0\\x-10=0\end{matrix}\right.\)
\(\left[{}\begin{matrix}x=-1\\x=10\end{matrix}\right.\)
Vậy \(x\) \(\in\){ -1; 10}

\(a,\Leftrightarrow x^3-8-x^3-2x=12\Leftrightarrow-2x=20\Leftrightarrow x=-10\\ b,\Leftrightarrow x^2-6x+9-x^2+4=16\Leftrightarrow=-6x=3\Leftrightarrow x=-\dfrac{1}{2}\\ c,\Leftrightarrow x\left(x^2-9\right)=0\\ \Leftrightarrow x\left(x-3\right)\left(x+3\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=3\\x=-3\end{matrix}\right.\\ d,\Leftrightarrow x^2\left(x-6\right)+9\left(x-6\right)=0\\ \Leftrightarrow\left(x^2+9\right)\left(x-6\right)=0\\ \Leftrightarrow x=6\left(x^2+9>0\right)\)

a) \(\text{Δ}=8^2-4.3.4=16\)
\(\left[{}\begin{matrix}x=\dfrac{-8+4}{2.3}=-\dfrac{2}{3}\\x=\dfrac{-8-4}{2.3}=-2\end{matrix}\right.\)

\(x^4-9x^3+x^2-9x=0\)
\(\Leftrightarrow x\left(x^2+1\right)\left(x-9\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x=9\end{matrix}\right.\)

Cách 1: x 2 − 9 x + 20 = 0
∆ =81-80=1>0 nên phương trình có hai nghiệm phân biệt x 1 = 9 + 1 2 = 5 ; x 2 = 9 − 1 2 = 4
Vậy phương trình có tập nghiệm S={4;5}
Cách 2:
x 2 − 9 x + 20 = 0 = 0 ⇔ x 2 − 5 x − 4 x + 20 = 0 ⇔ ( x − 5 ) ( x − 4 ) = 0 ⇔ x − 5 = 0 x − 4 = 0 ⇔ x = 5 x = 4
Vậy phương trình có tập nghiệm S={4;5}

\(a,\Leftrightarrow x\left(x+9\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\\ b,\Leftrightarrow\left(x+4-4\right)\left(x+4+4\right)=0\\ \Leftrightarrow x\left(x+8\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\\ c,\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\\ d,\Leftrightarrow\left(x-5\right)^2=0\Leftrightarrow x=5\)
a) \(\Leftrightarrow x\left(x+9\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-9\end{matrix}\right.\)
b) \(\Leftrightarrow x\left(x+8\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=-8\end{matrix}\right.\)
c) \(\Leftrightarrow x\left(x-4\right)\left(x+4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\\x=-4\end{matrix}\right.\)
d) \(\Leftrightarrow\left(x-5\right)^2=0\\ \Leftrightarrow x=5\)

\(x^2-9x+1=0\)
\(\Rightarrow\Delta=\left(-9\right)^2-4\cdot1\cdot1=77>0\)
\(\Leftrightarrow\left[{}\begin{matrix}x_1=\dfrac{9+\sqrt{77}}{2}\\x_2=\dfrac{9-\sqrt{77}}{2}\end{matrix}\right.\)
Ta có:
\(V=x^4+x^2+\dfrac{1}{5}x^2=x^4+\dfrac{6}{5}x^2\)
Thay \(x_1,x_2\) vào V ta có:
\(V_1=\left(\dfrac{9+\sqrt{77}}{2}\right)^4+\dfrac{6}{5}\left(\dfrac{9+\sqrt{77}}{2}\right)^2\approx6333\)
\(V_2=\left(\dfrac{9-\sqrt{77}}{2}\right)^4+\dfrac{6}{5}\left(\dfrac{9-\sqrt{77}}{2}\right)^2\approx0,015\)

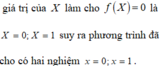
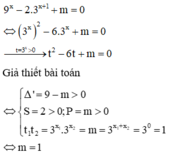
\(x^2-9x=0\)
\(\Rightarrow x\left(x-9\right)=0\)
\(\Rightarrow\orbr{\begin{cases}x=0\\x-9=0\Rightarrow x=9\end{cases}}\)
KL : x = 0 hoặc x = 9