Trên hình bên cho biết : AB = DC , AD = BC.
CMr: AB//DC,AD//BC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
31 tháng 1 2022
Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)
CM
23 tháng 7 2018
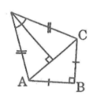
a. Nối AC và kẻ DH ⊥ AC
Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
A C 2 = A B 2 + B C 2 = 12 2 + 12 2 = 144 + 144 = 288
Suy ra: AC = 12 2 (cm)
Ta có: ∆ ACD cân tại D
DH ⊥ AC
DL
2
6 tháng 1 2021
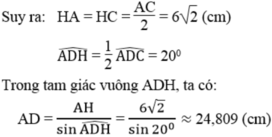
Áp dụng định lý Py-ta-go vào tam giác vuông OAB, ta được:
\(AB^2=OB^2+OA^2\)(1)
Áp dụng định lý Py-ta-go vào tam giác vuông ODC, ta được:
\(DC^2=OD^2+OC^2\)(2)
Từ (1) và (2) -> \(AB^2+CD^2=OA^2+OB^2+OC^2+OD^2\left(3\right)\)
Áp dụng đính lý Py-ta-go vào tam giác vuông OBC, ta được:
\(BC^2=OC^2+OB^2\left(4\right)\)
Áp dụng định lý Py-ta-go vào tam giác vuông OAD, ta được:
\(AD^2=OA^2+OD^2\left(5\right)\)
Từ (4) và (5) ta có: \(BC^2+AD^2=OB^2+OC^2+OA^2+OD^2\left(6\right)\)
Từ (3) và (6) suy ra \(AB^2+DC^2=BC^2+AC^2\)
Mỏi tay vc:vv
TQ
0
24 tháng 3 2023
Sửa đề: đường cao BH
a: Xét ΔBDC vuông tại B và ΔHBC vuông tại H có
góc C chung
=>ΔBDC đồng dạng với ΔHBC
b: \(BD=\sqrt{25^2-15^2}=20\left(cm\right)\)
HC=15^2/25=9cm
HD=25-9=16cm
10 tháng 4 2022
a) Nối A với F 
Và D với F
Ta có:
ED=1/3 AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
a) Nối A với F
Và D với F
Ta có:
ED=1/3 AD
=> ED= ½ AD
S(EFD) = 1/3 S(AFD)
Vì đáy ED= 1/3 AD ; d.c hạ từ F chung
Nếu lấy EF làm đáy => đ.c hạ từ D= 1/3 đ.c hạ từ A
=>đ.c của tam giác EFD là 30 x 1/3 = 10 = đ.c của tam giác FCD
=>đ.c của tam giác AEF là 30 x (1 – 1/3 ) = 20 = đ.c của tam giác ABF
S(ABF) = 60 x 20 : 2 = 600 cm2
S ( FCD)= 90 x 10 : 2 =450 cm2
S ( ABCD)= (90+60) x 30 : 2 = 2250 cm2
Mà S( AFD ) = S(ABCD) – S (ABF) – S (FCD)
S (AFD )= 2250 – 600 – 450 = 1200 cm2
S(EFD ) = 1200 : 3 = 400
=> S(EDFC) = 400 + 450 = 850 (cm2)
b) S(EFD ) / S( FCD) = 400/450 = 8/9
vậy EF = 8/9 CD
CM
23 tháng 9 2019
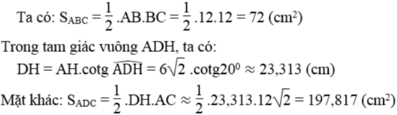
Vậy S d i ề u = S A B C + S A D C = 72 + 197 , 817 = 269 , 817 c m 2