Cho x + y = 1 . Tính giá trị của bt \(x^3+3xy+y^3\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan
NQ
0

NT
2

NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
b; 13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\).y + 3\(xy^2\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
NT
a) cho x+y=1. Tính giá trị biểu thức x^3+ y^3+ 3xy
b) cho x-y=1. Tính giá trị biểu thức x^3- y^3- 3xy
2

BT
30 tháng 6 2018
x^3+ y^3+ 3xy
=(x+y)(x^2 -xy + y^2 ) + 3xy
=x^2 -xy + y^2 + 3xy
=x^2 + 2xy + y^2
=(x+y)^2 =1
=> x^3+ y^3+ 3xy=1

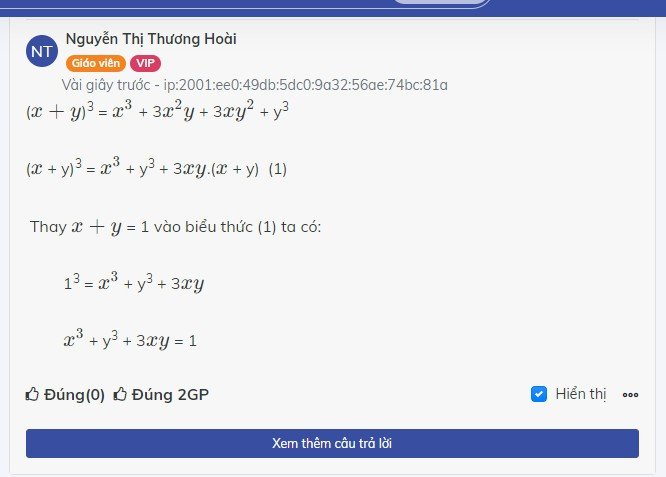
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x+y\))3 = \(x^3\) + 3\(x^2\)y + 3\(xy^2\) + y3 = \(x^3\)+y3+3\(xy\)(\(x+y\))
1 = \(x^3\)+y3+3\(xy\)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
12 tháng 7 2024
13 = (\(x-y\))3 = \(x^3\) - 3\(x^2\)y + 3\(xy\) - y3 = \(x^3\) - y3 - 3\(xy\)(\(x-y\))
1 = \(x^3\) - y3 - 3\(xy\)
Z
2

TN
13 tháng 6 2016
Từ x+y=1 (GT)
=>(x+y)3=13=1
=>x3+3x2y+3xy2+y3=1 (HĐT)
=>x3+y3+3xy(x+y)=1
=>x3+y3+3xy*1=1
=>x3+y3+3xy=1
13 tháng 6 2016
từ x+y=1=>x=1-y
thay vào biểu thức trên ta được: (1-y)^3+3(1-y)y+y^3=1-3y+3y^2-y^3+3y-3y^2+y^3=1
\(x^3+3xy+y^3\)
\(=\left(x+y\right)\left(x^2-xy+y^2\right)+3xy\)
\(=x^2+y^2-xy+3xy\)
\(=x^2+2xy+y^2\)
\(=\left(x+y\right)^2\)
\(=1^2\)
\(=1\)
\(x^3+3xy+y^3=x^3+3xy.1+y^3\)
\(=x^3+3xy\left(x+y\right)+y^3\)
\(=x^3+3x^2y+3xy^2+y^3\)
\(=\left(x+y\right)^3=1\)