tính nhanh 1x30+2x29+3x28+...+30.1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
0
TT
2
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
27 tháng 9 2021
\(A=2\left(1.30+2.29+3.28+...+15.16\right)=\)
\(=2.\left[1.30+2.\left(30-1\right)+3.\left(30-2\right)+...+15.\left(30-14\right)\right]=\)
\(=2.\left(1.30-1.2+2.30+3.30-2.3+4.30-3.4+...+15.30-14.15\right)=\)
\(=2.\left[30.\left(1+2+3+...+15\right)-\left(1.2+2.3+3.4+...+14.15\right)\right]=\)
Đặt \(B=1+2+3+...+15=\frac{15.\left(1+15\right)}{2}=120\)
Đặt \(C=1.2+2.3+3.4+...+14.15\)
\(\Rightarrow3C=1.2.3+2.3.3+3.4.3+...+14.15.3=\)
\(=1.2.3+2.3.\left(4-1\right)+3.4.\left(5-2\right)+...+14.15.\left(16-13\right)=\)
\(=1.2.3-1.2.3+2.3.4-2.3.4+3.4.5-...-13.14.15+14.15.16=14.15.16\)
\(\Rightarrow C=\frac{14.15.16}{3}=5.14.16=1120\)
\(\Rightarrow A=2.\left(30.B-C\right)=2\left(30.120-1120\right)=4960\)
HN
2 tháng 1 2022
a, 2000+(32,4-2,8)x0,25=2000+29,6x0,25
=2000+7,4
=2007,4
b, 97x29+29x2+29=2813+59+29
=2900
c, 200:2x29=100x29
=2900
CM
25 tháng 8 2019
Chọn B
Ta có:
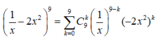
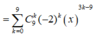
Hệ số cuả số hạng chứa x 6 tương ứng với 6 = 3k - 9 => k = 5
Vậy hệ số cuả số hạng chứa x 6 là C 9 5 . 2 5
S
18 tháng 5 2017
Ta có:
A=\(\frac{1}{1.101}+\frac{1}{2.102}+...+\frac{1}{25.125}\)
=\(\frac{1}{100}\left(\frac{100}{1.101}+\frac{100}{2.102}+...+\frac{100}{25.125}\right)\)
=\(\frac{1}{100}\left(1-\frac{1}{101}+\frac{1}{2}-\frac{1}{102}+...+\frac{1}{25}-\frac{1}{125}\right)\)
=\(\frac{1}{100}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
B=\(\frac{1}{1.26}+\frac{1}{2.27}+...+\frac{1}{100.125}\)
=\(\frac{1}{25}\left(\frac{25}{1.26}+\frac{25}{2.27}+...+\frac{25}{100.125}\right)\)
=\(\frac{1}{25}\left(1-\frac{1}{26}+\frac{1}{2}-\frac{1}{27}+...+\frac{1}{100}-\frac{1}{125}\right)\)
=\(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{100}\right)-\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{125}\right)\right]\)
=\(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)+\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{100}\right)-\left(\frac{1}{26}+\frac{1}{27}+...+\frac{1}{100}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
= \(\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]\)
=> \(\frac{A}{B}\)=\(\frac{\frac{1}{100}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]}{\frac{1}{25}\left[\left(1+\frac{1}{2}+...+\frac{1}{25}\right)-\left(\frac{1}{101}+\frac{1}{102}+...+\frac{1}{125}\right)\right]}\)=\(\frac{1}{\frac{100}{\frac{1}{25}}}\)=\(\frac{1}{100}\cdot25=\frac{25}{100}=\frac{1}{4}\)
