Tam giác CDE vuông tại C có đường cao CI. Chứng minh rằng CE.CD = DE.CI
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 5 2022
a: Xét ΔCDH vuông tại H và ΔCAH vuông tại H có
CH chung
HD=HA
Do đó: ΔCDH=ΔCAH
b: Xét ΔCDA có CD=CA
nên ΔCDA cân tại C
mà \(\widehat{D}=60^0\)
nên ΔCDA đều
30 tháng 12 2020
Ta có: HI/CH=1/2 HK / CH = EK / 2 EH = EK/DE
tam giác HIC đồng dạng tam giác EKD vì HI/CH=EK/DE và góc CHI = góc DEK ( cùng phụ góc HCK)
suy ra góc HCI = góc EDK
ta có: góc KDC + góc DCI = góc KDC + ( Góc HCI + góc HCD)
=(góc KDC + góc EDK) + góc HCD
= góc HDC + góc HCD
= 90 độ
suy ra DK vuông góc CI
CM
7 tháng 12 2018
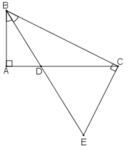
+) Ta có BD là tia phân giác của góc ABC nên: ∠(ABD) = ∠(DBC) (1)
+ Lại có: ∠(ADB)= ∠(CDE) ( hai góc đối đỉnh) (2)
+) Tam giác ABD vuông tại A nên:
∠ (ABD) + ∠(ADB) = 90° (tính chất tam giác vuông) (3)
Từ (1); (2) và (3) suy ra: ∠ (DBC) + ∠(CDE) = 90° (4)
+) Tam giác BCE vuông tại C nên:
∠ (DBC) + ∠(BEC) = 90° (tính chất tam giác vuông) (5)
Từ (4) và (5) suy ra : ∠ (CDE) = ∠(BEC)
Vậy tam giác CDE có hai góc bằng nhau.
TrướcSau
4 tháng 4 2021
1) Xét ΔCDE vuông tại D và ΔAHB vuông tại H có
\(\widehat{DCE}=\widehat{HAB}\left(=90^0-\widehat{ABC}\right)\)
Do đó: ΔCDE\(\sim\)ΔAHB(g-g)
1 tháng 8 2021
a) Xét ΔBHA vuông tại H và ΔBAC vuông tại A có
\(\widehat{ABH}\) chung
Do đó: ΔBHA\(\sim\)ΔBAC(g-g)
Suy ra: \(\dfrac{BA}{BC}=\dfrac{BH}{BA}\)
hay \(BA^2=BH\cdot BC\)
b) Xét ΔCHI vuông tại H và ΔCKB vuông tại K có
\(\widehat{ICH}\) chung
Do đó: ΔCHI\(\sim\)ΔCKB(g-g)
Suy ra: \(\dfrac{CH}{CK}=\dfrac{CI}{CB}\)
hay \(CH\cdot CB=CK\cdot CI\)
C D E I
Em xét hai tam giác đồng dạng DEC và DCI
\(S_{ABC}=\frac{CE.CD}{2},S_{ABC}=\frac{DE.CI}{2}\Rightarrow CE.CD=DE.CI\)