Tìm x: \(x^4+\sqrt{x^2+13}-13=0\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
3
ND
0
PT
1
4 tháng 7 2019
\(\sqrt{x^2-6x+13}=0\)
\(\Leftrightarrow x^2-6x+13=0\)
\(\Leftrightarrow x^2-6x+9+4=0\)
\(\Leftrightarrow\left(x-3\right)^2+4=0\)
Mà: \(\left(x+3\right)^2+4\ge4>0\forall x\)
=> Không có giá trị của x thỏa mãn
\(\sqrt{x^2+4}=x+2\)
\(\Leftrightarrow\hept{\begin{cases}x^2+4=\left(x+2\right)^2\\x+2>0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x^2+4=x^2+4x+4\\x>-2\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=0\left(tm\right)\\x>-2\end{cases}}\)
Vậy: PT có tập nghiệm S = { 0 }
=.= hk tốt!!
TN
27 tháng 6 2018
Câu 1) x\(^2\) - 5 = 0
\(\Leftrightarrow\)(x - \(\sqrt{5}\))(x + \(\sqrt{5}\)) = 0
\(\Leftrightarrow\)x = \(\sqrt{5}\) hoặc
x = -\(\sqrt{5}\)
Câu 2) x\(^2\) - \(2\sqrt{13}x\) +13 = 0
\(\Leftrightarrow\)(x - \(\sqrt{13}\))\(^2\) = 0
\(\Leftrightarrow\)x - \(\sqrt{13}\) = 0
\(\Leftrightarrow\)x = \(\sqrt{13}\)
Câu 3) \(\left(x+2\right)\sqrt{x-3}=0\)
\(\Leftrightarrow x=-2\) hoặc
\(x=3\)
Câu 4) Tới lúc này mình hơi lười nên bạn tự giải phương trình nhé.
Hướng dẫn: Ta biết nếu\(\sqrt{x}\) = a với a\(\ge\) 0 thì x= a\(^2\), nên ta đưa về tìm x thỏa mãn (x + \(\sqrt{x-2}\))\(^2\) = 4(x-1)
Giải phương trình này ta có x=2.
Câu 5)\(\sqrt{9-12x+4x^2}=4\)
\(\Leftrightarrow\sqrt{\left(3-2x\right)^2}=4\)
\(\Leftrightarrow\left|3-2x\right|=4\)
\(\Leftrightarrow3-2x=4\) hoặc
-3 + 2x = 4
\(\Leftrightarrow\) x= -0.5 hoặc x= 3.5
5 tháng 2 2022
a: \(=6+2\sqrt{11}-4+\sqrt{11}=2+3\sqrt{11}\)
b: \(=\dfrac{3x+9\sqrt{x}-2x+4\sqrt{x}}{\left(\sqrt{x}+3\right)\left(x-2\sqrt{x}\right)}\cdot\dfrac{\left(\sqrt{x}+3\right)^2}{\sqrt{x}+13}=\dfrac{\sqrt{x}+3}{x-2\sqrt{x}}\)
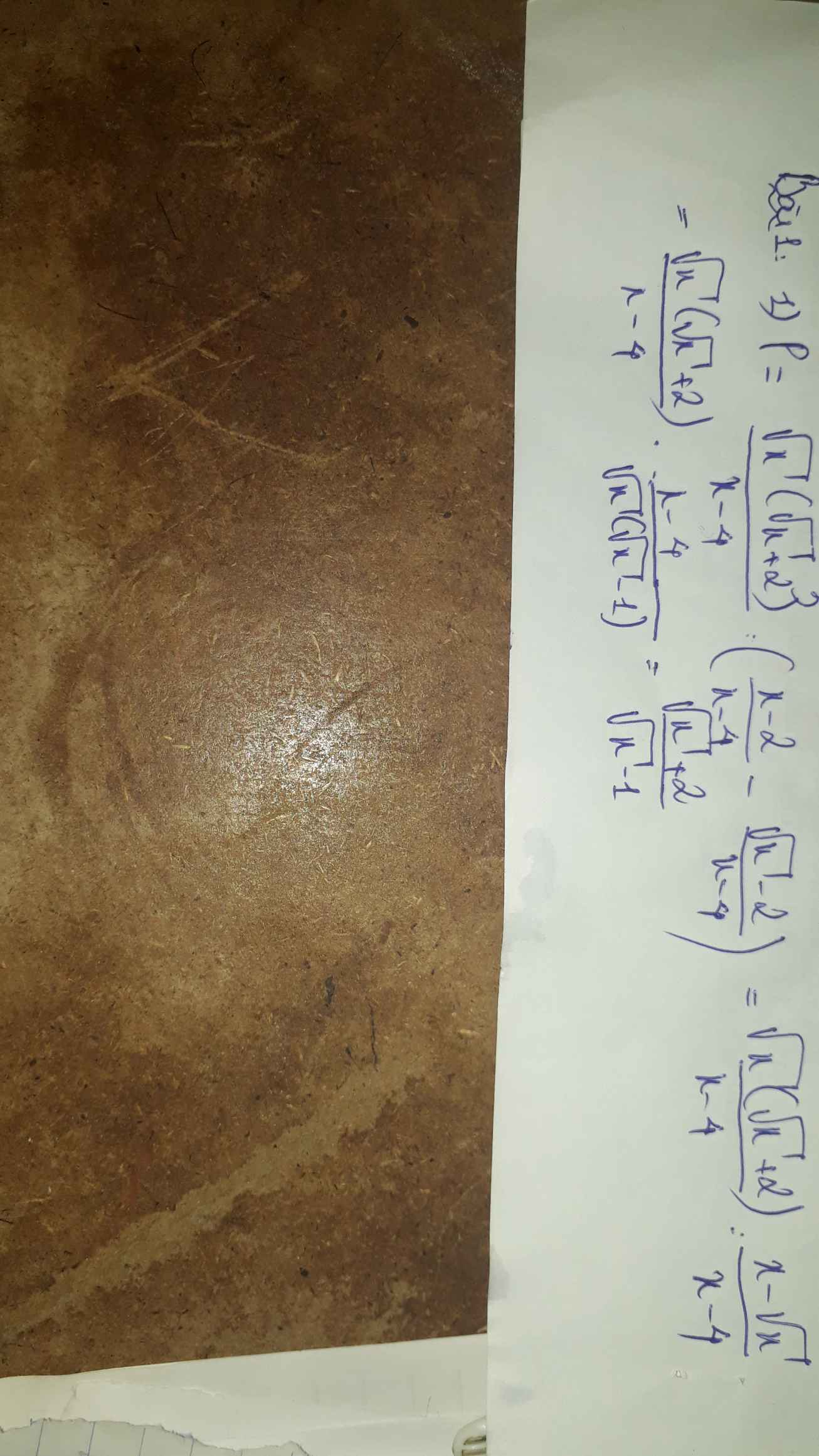
Đặt \(x^2+13=t\Leftrightarrow x^2=t-13\).Thay vào,ta có:
\(PT\Leftrightarrow\left(t-13\right)^2+\left(t-13\right)=0\)
Mà \(\left(t-13\right)^2\ge0\) nên \(\left(t-13\right)^2+\left(t-13\right)\ge0\)
Dấu "=" xảy ra \(\Leftrightarrow-\left(t-13\right)^2=t-13\)
Dễ giải được t = 12. Suy ra \(x^2=t-13=12-13=-1\)
Suy ra phương trình vô nghiệm. (do \(x^2\ge0\forall x\))
Vậy \(x\in\varnothing\)