Cho hình chữ nhật ABCD có đường chéo AC = 11 cm và AD = 4 cm.
Độ dài BD = cm và CB = cm.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TN
31 tháng 3 2020
gọi chiều dài, chiều rộng và đường chéo của hình chữ nhật đó lần lượt là a,b,c . Áp dụng định lí Pitago ta có
:\(a^2+b^2=c^2\)
\(4^2+6^2=c^2\)
\(=>c^2=52\)
\(=>c=\sqrt{52}=7,2cm\)
Học tốt
TN
31 tháng 3 2020
Bổ sung câu trả lời của mk nha:
vậy độ dài đường chéo bằng 7,2 cm
7 tháng 3 2022
Độ dài đường chéo là: \(\sqrt{4^2+3^2}=5\left(cm\right)\)
CM
27 tháng 12 2019
a) Vẽ hình chữ nhật ABCD có chiều dài 4 cm, chiều rộng 3 cm. Sau đó nối đỉnh A với đỉnh C, đỉnh B, đỉnh D.
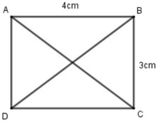
b) Đo chiều dài đoạn thẳng
AC, BD rồi viết số thích hợp vào chỗ chấm:
- AC = 5 cm
- BD = 5 cm
c) Nhận xét:
Độ dài AC = độ dài BD
(AC, BD là hai đường chéo của hình chữ nhật)
CM
23 tháng 11 2019
Độ dài đường chéo BD là:
40×35=24(cm)
Diện tích hình thoi ABCD là:
40×24:2=480( c m 2 )
Vì hình chữ nhật GHIK có diện tích bằng diện tích hình thoi ABCD nên diện tích hình chữ nhật GHIK là 480 c m 2 .
Chiều dài hình chữ nhật là:
480:15=32(cm)
Chu vi hình chữ nhật là:
(32+15)×2=94(cm)
Đáp số: 94cm.
Vậy đáp án đúng điền vào ô trống là 94.
25 tháng 6 2021
Bài 1 : A B C D 4
Vì ABCD là hình vuông \(\Rightarrow\widehat{DAB}=\widehat{ABC}=\widehat{BCD}=\widehat{CDA}=90^0\)
\(\Rightarrow AB=BC=CD=AD=4\)cm
Áp dụng định lí pytago tam giác ADC vuông tại D ta có :
\(AC^2=AD^2+CD^2=16+16=32\Rightarrow AC=4\sqrt{2}\)cm
Vì ABCD là hình vuông nên 2 đường chéo bằng nhau AC = BD = 4\(\sqrt{2}\)cm
25 tháng 6 2021
Bài 2 :
A B C D 3 căn27
Vì ABCD là hình chữ nhật nên \(AB=CD;AD=BC\)
Áp dụng định lí Pytago tam giác ACD vuông tại D ta có :
\(AC^2=AD^2+DC^2=27+9=36\Rightarrow AC=6\)cm
14 tháng 8 2016
gọi chiều dài là a, chiều rộng là b,đường chéo là c
ta có : c^2=a^2+b^2
=> 25^2=a^2+b^2
vì b=3/4.a
=> a^2+(3/4.a)^2=625
=> a^2+9/16.a^2=625
=> a^2+(1+9/16)=625
=> a^2 . 25/16 =625
=> a^2 =400
=> a =20
=> b =15
vậy chiều dài là 20cm,chiều rộng là15cm
Vì ABCD là hcn
=> AC = BD = 11 (cm)
BC = AD = 4 cm
4cm ban nhe