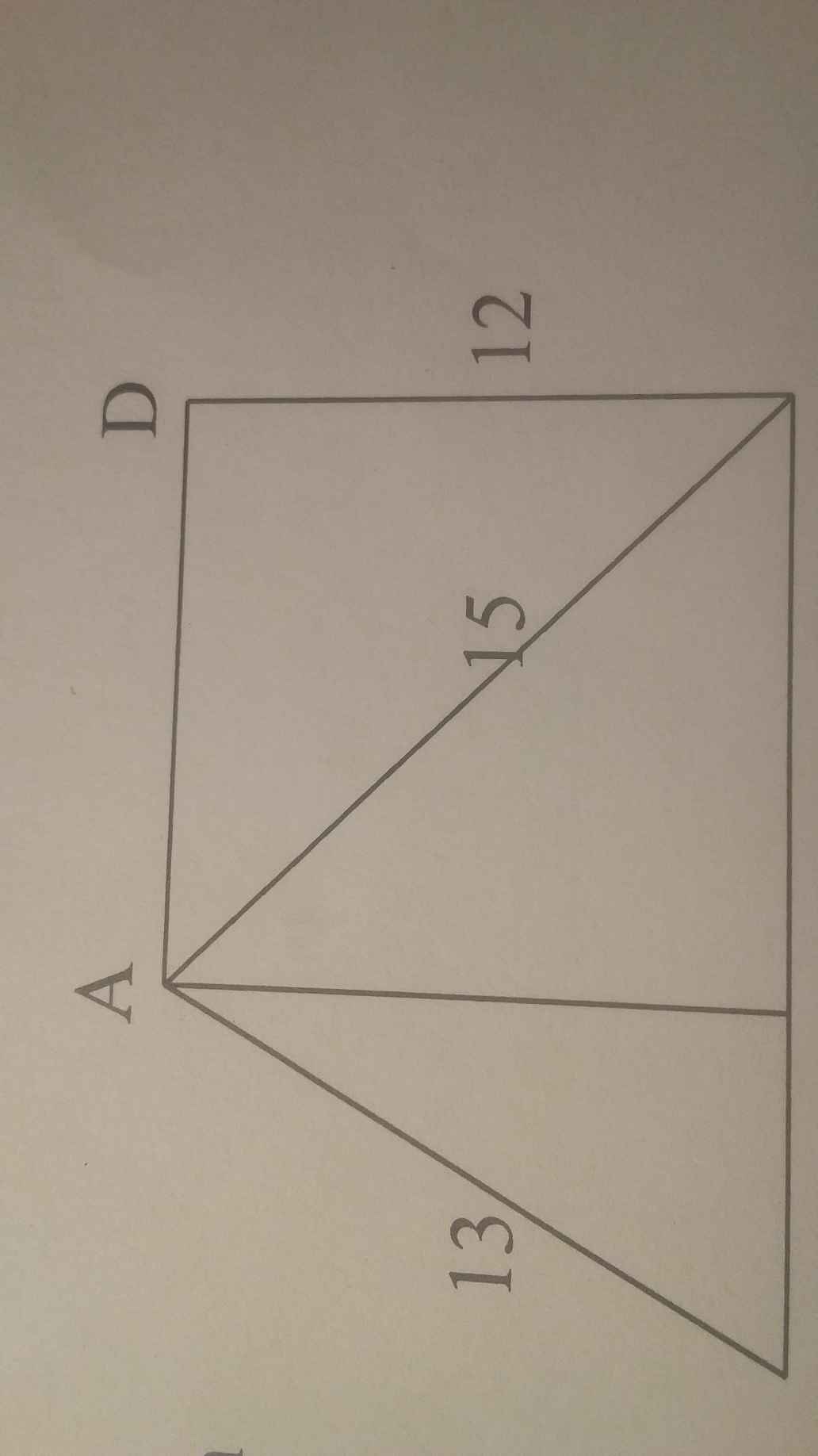
Biết AD \(\perp\)DC, DC \(\perp\)BC, AB = 13 cm, AC = 15 cm, DC = 12 cm. Tính độ dài đoạn thẳng BC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Xét tứ giác \(ADCH\) có:
\(\widehat{D}=\widehat{C}=\widehat{H}=90^o\)
\(\Rightarrow ADCH\) là hình chữ nhật
\(\Rightarrow AH=DC=12cm\)
Xét \(\Delta ADC\left(\widehat{D}=90^o\right)\) có:
\(AC^2=AD^2+DC^2\) (định lí pitago)
\(\Rightarrow AD=\sqrt{AC^2-DC^2}=\sqrt{15^2-12^2}=9cm=HC\)
Xét \(\Delta ABH\left(\widehat{H}=90^o\right)\) có:
\(AB^2=AH^2+BH^2\) (định lí pitago)
\(\Rightarrow BH=\sqrt{AB^2-AH^2}=\sqrt{13^2-12^2}=5cm\)
\(\Rightarrow BC=BH+HC=5+9=14cm\)
Vậy \(BC=14cm\)

Đặt \(\left\{{}\begin{matrix}BD=x\\CD=y\end{matrix}\right.\) với x;y là các số nguyên dương
Áp dụng định lý phân giác:
\(\dfrac{BD}{AB}=\dfrac{CD}{AC}\Rightarrow\dfrac{x}{35}=\dfrac{y}{50}\Rightarrow y=\dfrac{10x}{7}\)
Do \(y\) nguyên và 10;7 nguyên tố cùng nhau \(\Rightarrow x\) chia hết cho7
Mặt khác theo BĐT tam giác:
\(BC< AB+AC\Rightarrow x+y< 85\)
\(\Rightarrow x+\dfrac{10x}{7}< 85\Rightarrow x< 35\)
BC lớn nhất khi x lớn nhất, số nguyên chia hết cho 7 và nhỏ hơn 35 lớn nhất là 28
Vậy \(x_{max}=28\Rightarrow BC_{max}=28+\dfrac{10.28}{7}=68\)

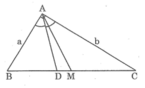
a,Ta có : AD là phân giác \(\widehat{BAC}\)
\(\Rightarrow\dfrac{BD}{DC}=\dfrac{AB}{AC}\)
hay \(\dfrac{4}{DC}=\dfrac{12}{15}\)
\(\Rightarrow DC=\dfrac{4.15}{12}=5\left(cm\right)\)
b, Ta có : \(BC=BD+DC=4+5=9\left(cm\right)\)
Ta có : DE//AB
\(\Rightarrow\dfrac{DC}{BC}=\dfrac{DE}{AB}\left(hệ\cdot quả\cdotđịnh\cdot lý\cdot ta-lét\right)\)
hay \(\dfrac{5}{9}=\dfrac{DE}{12}\)
\(\Rightarrow DE=\dfrac{5.12}{9}=\dfrac{20}{3}\left(cm\right)\)

Áp dụng định lí Pi-ta-go vào tam giác vuông ABC, ta có:
B C 2 = A B 2 + A C 2 = a 2 + b 2
Suy ra: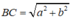
Ta có: AM = BM = 1/2.BC (tính chất đường trung tuyến ứng với cạnh huyền).
Suy ra: AM = 1/2 a 2 + b 2
Vì AD là đường phân giác của ∠(BAC) nên:
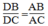 (tính chất đường phân giác)
(tính chất đường phân giác)
Suy ra: 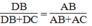
hay 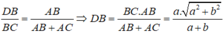
Vậy
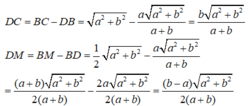
Ở bài này chỉ tính được giá trị xấp xỉ thôi chứ không tính chính xác được nha!Phải thêm điều kiện tam giác ABC mới làm đc
A B C 13 cm 15 cm D 12 cm
*Tính AD
Xét tam giác ADC vuông tại D.Áp dụng định lí Pytago,ta có: \(AD^2+DC^2=AC^2\Leftrightarrow AD^2=AC^2-DC^2=15^2-12^2=81\)
Suy ra AD = 9 cm
*Tính BD
Xét tam giác ADB vuông tại D. Theo định lí Pytago thì:\(BD^2+AD^2=AB^2\)
Hay \(BD^2=AB^2-AD^2=13^2-9^2=88\) cm
Suy ra \(BD=\sqrt{88}\approx9\) cm
*Tính BC
Mà \(BC=BD+DC\approx9+12=21\) cm
Vậy ...