Cho AB là đường kính của (O; R), C thuộc (O) (C khác A, B). Kẻ CH⊥AB tại H. I là trung điểm của AC. OI cắt tiếp tuyến tại A của (O) ở M (nghĩa là kẻ tiếp tuyến Ax chẳng hạn rồi kéo dài OI để cắt Ax tại M). MB cắt CH tại K.
C/m a) MC là tiếp tuyến của (O)
b) C, H, O, I thuộc một đường tròn
c) K là trung điểm của CH.
Các bạn giúp mình bài này nhé, mình xin cảm ơn ^ ^
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Gọi E là trung điểm của OA
=>E là tâm đường tròn đường kính OA
Xét (E) có
ΔOBA nội tiếp
OA là đường kính
Do đó: ΔOBA vuông tại B
=>AB vuông góc OB tại B
=>AB là tiếp tuyến của (O)
Xét (O) có
ΔOCA nội tiếp
OA là đường kính
Do đó: ΔOCA vuông tại C
=>AC vuông góc với CO tại C
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBCK nội tiếp
BK là đường kính
Do đó: ΔBCK vuông tại C
=>BC vuông góc CK tại C
Xét (E) có
ΔBCI nội tiếp
BI là đường kính
Do đó: ΔBCI vuông tại C
=>BC vuông góc CI tại C
\(\widehat{KCI}=\widehat{KCB}+\widehat{ICB}\)
\(=90^0+90^0\)
\(=180^0\)
=>K,C,I thẳng hàng
Xét (B;BC) có
BC là bán kính
KI vuông góc với BC tại C
Do đó: KI là tiếp tuyến của (B;BC)

Đầu tiên, với điều kiện AC^2 = BC, ta có thể suy ra AC = BC. Do đó, tam giác ABC là tam giác cân tại A và B.
Tiếp theo, vì CD vuông góc AB, ta có thể suy ra tam giác ACD và tam giác BCD là tam giác vuông.
Do DE là đường kính của đường tròn O, nên tam giác ADE và tam giác BDE là tam giác vuông tại D và E.
Vì tam giác ABC là tam giác cân, ta có thể suy ra tỉ số diện tích DCE và ABD bằng tỉ số diện tích tam giác DCE và tam giác ABD.
Tuy nhiên, để tính diện tích của các tam giác này, chúng ta cần biết thêm thông tin về kích thước của các đoạn thẳng và góc giữa chúng.
Vì vậy, để tìm tỉ số diện tích DCE và ABD, cần có thêm thông tin chi tiết về hình học của hình và các giá trị số cụ thể.

a: ΔOAB cân tại O
mà OC là đường cao
nên OC là phân giác của góc AOB
Xét ΔOAC và ΔOBC có
OA=OB
góc AOC=góc BOC
OC chung
Do đó: ΔOAC=ΔOBC
=>góc OBC=90 độ
=>CB là tiếp tuyến của (O)
b: Xét (O) có
ΔBAD nôi tiếp
BD là đường kính
Do đó:ΔBAD vuông tại A
=>AD vuông góc với BA
=>AD//CB

a: ΔOAB cân tại O
mà OI là đường trung tuyến
nên OI vuông góc AB
I là trung điểm của AB
=>IA=IB=16/2=8cm
ΔOIA vuông tại I
=>OA^2=OI^2+IA^2
=>OI^2=10^2-8^2=36
=>OI=6(cm)
b: OM=OI+IM
=>6+IM=10
=>IM=4cm
ΔMIA vuông tại I
=>MI^2+IA^2=MA^2
=>\(MA=\sqrt{4^2+8^2}=4\sqrt{5}\left(cm\right)\)

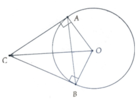
a, ∆OAC = ∆OBC (c.g.c)
=> O B C ^ - O A B ^ = 90 0
=> đpcm
b, Sử dụng hệ thức lượng trong tam giác vuông OBC tính được OC=25cm

a) Vì TO là đường kính \(\Rightarrow\angle TMO=90\) mà \(M\in\left(O\right)\Rightarrow TM\) là tiếp tuyến của (O)
b) Xét \(\Delta TMC\) và \(\Delta TDM:\) Ta có: \(\left\{{}\begin{matrix}\angle MTDchung\\\angle TMC=\angle TDM\end{matrix}\right.\)
\(\Rightarrow\Delta TMD\sim\Delta TCM\left(g-g\right)\Rightarrow\dfrac{TC}{TM}=\dfrac{TM}{TD}\Rightarrow TC.TD=TM^2\)
c) Vì đường tròn đường kính TO có tâm I và đường tròn (O) cắt nhau tại M và N \(\Rightarrow\) IO là trung trực của MN \(\Rightarrow MN\bot TO\)
mà \(\Delta TMO\) vuông tại M \(\Rightarrow TM^2=TE.TO\) (hệ thức lượng)
mà \(TC.TD=TM^2\Rightarrow TC.TD=TE.TO\Rightarrow\dfrac{TC}{TE}=\dfrac{TO}{TD}\)
Xét \(\Delta TEC\) và \(\Delta TDO:\) Ta có: \(\left\{{}\begin{matrix}\angle OTDchung\\\dfrac{TC}{TE}=\dfrac{TO}{TD}\end{matrix}\right.\)
\(\Rightarrow\Delta TEC\sim\Delta TDO\left(c-g-c\right)\Rightarrow\angle TEC=\angle TDO\Rightarrow ODCE\) nội tiếp